How to Win at Fortress
Fortress is a traditional solitaire, one of the oldest open solitaires (games where all of the cards are dealt only once, face up, at the start), and at one time one of the most popular: Alphonse Moyse Jr., in 150 Ways To Play Solitaire (1950), calls Fortress "perhaps the most popular of those in which the whole pack is laid out." It dates back at least as far as Lady Adelaide Cadogan's Illustrated Games of Patience, one of the first English-language books on solitaire, which was published in the 1870's. Originally a French game (La Forteresse), it is one of only four one-deck games in Lady Cadogan's original book. The deck is dealt out into ten rows of five cards each, the two extra cards going on the first two rows. The four foundation piles are built up in suit from ace to king; the ten tableau rows can be packed in suit either up or down. That is, if the seven and eight of clubs are both uncovered, either card may be placed on the other. An uncovered card from any of the other rows may be placed in an empty row -- this is an important point missed by some computer implementations, which only allow kings to be placed in an empty row (making the game essentially unplayable). Only one card at a time can be moved; we'll see how this works later. Some packages make the game too easy by allowing the tableau to be packed regardless of suit (as in Beleaguered Castle, a later offshoot of Fortress) and allowing any rank to be selected as the starting rank for the foundations (as in the variant Chessboard). There is nothing wrong with these games, but Fortress provides a very challenging game when played by the traditional rules. At one point in the early days of Windows solitaire, there were no correct versions of Fortress. Nowadays the game is correctly programmed in several of the better packages, including BVS Solitaire, Pretty Good Solitaire and Solitude for Windows.

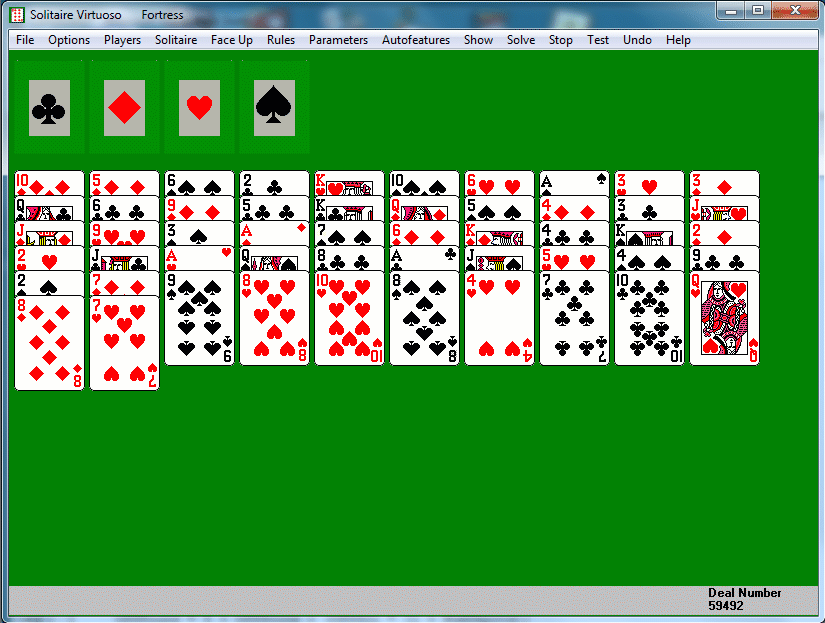
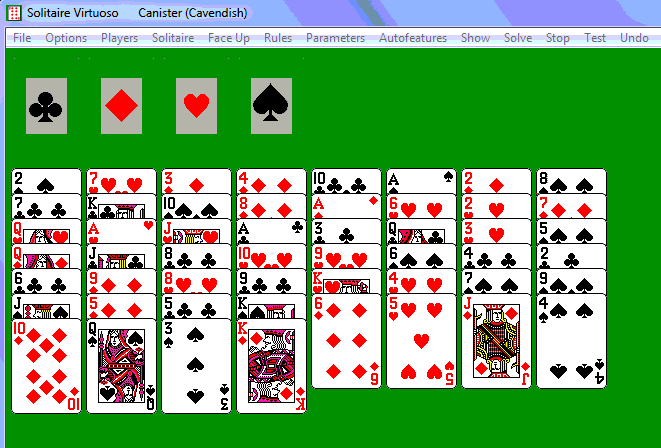
The Solitaire Virtuoso program now has a working version of
Fortress with a nice added feature: sequences automatically
reverse when they are either selected and moved onto another card, or
right-clicked and sent to an empty column. Above is an example deal,
number 59492 from Virtuoso. Here the tableau
is
simply dealt in ten columns. There are no aces uncovered at the start;
if
any become uncovered, they will automatically move to the foundations,
along with any succeeding cards in suit (since this is a single-deck
game with packing in suit, there is never a disadvantage to playing
every possible card to the foundations, though Autoplay can be turned
off if desired). The program also keeps a written solution
(the display of this can be turned on or off at will), using
a simplified version of standard FreeCell notation: every move is
recorded as two numbers, showing the starting and ending column of each
move (using A to indicate column 10). Cards which go to the
foundations automatically are not recorded in the solution.
Having aces available at the start is not necessarily that
valuable; what we want is lots of cards of adjacent ranks in the same
suit, which can be played on each other. If we cannot clear at least
one column fairly
quickly, there is no hope of a win. We
see here that there are two hearts of adjacent ranks (78) and two
spades (89). This is not usually too promising, but if we look
carefully at column 2, there are lots of cards adjacent in rank and
suit to cards which are already uncovered, or which can be uncovered
quickly. In fact, we can clear the whole column with a quick set
of moves. Put the seven of hearts on the eight, the seven of
diamonds on the eight, the jack of clubs on the ten, the nine of hearts
on the ten, and the six of clubs on the seven. Now put the eight
of spades from column 6 on the nine, uncovering the ace of clubs (which
goes to the foundation), the newly exposed six of diamonds on the
seven, and the five of diamonds on the six. Now we have an
empty column, a promising start (though many games are still lost even
after clearing a whole column). We have turned on the
solution display in the screenshot below. If we can clear a
second column, the chances of winning become much higher.
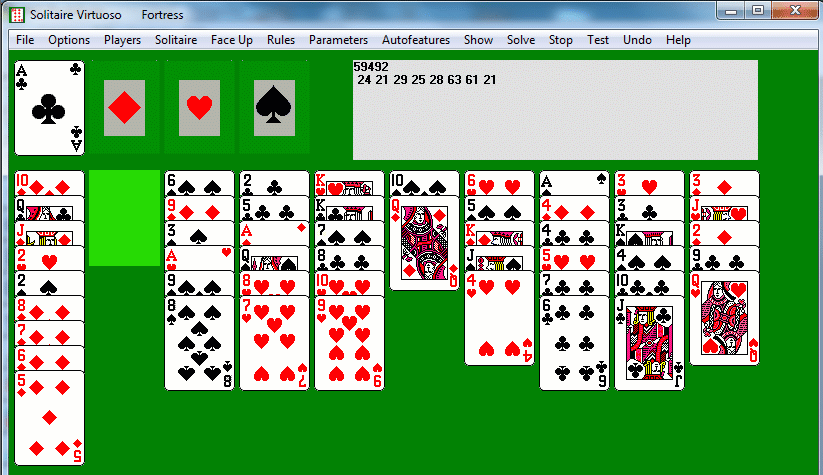
Since only one card at a time can be moved, we can't take the
seven-eight of hearts as a group and simply place it directly onto the
nine-ten. But since we now have an empty column, we can move it
there via reversal, which is a
hallmark of Fortress. Right-click on the seven or eight of hearts
(actually anywhere in column 4, since the program knows which cards can
move), and the seven of hearts moves to the empty column 2, followed
automatically by the eight. [There are actually two
ways of moving a card or sequence to an
empty column: either right-click, which sends all available cards in
reverse order to the first empty column, or simply click to select, and
click on the empty column where you want the card(s) to go.] Now click
normally (i.e. left-click) on either the seven of eight of hearts
(selecting and highlighting both), and click on the nine of hearts to
move them both there in correct sequence. Now if we move the
queen of spades to column 2, which is empty again, the ace of diamonds
will go to the foundation, we can play the five of clubs onto the six,
and the two of clubs goes to the foundation. We've traded one
empty column for another, but made some progress.
We want to clear a second column, but there doesn't seem any obvious
way to do so, nor are there any obvious free moves which will make
progress without using up our empty column. Column 8 looks
promising, but if we simply reverse the five-six-seven of clubs into
the empty column and play the five of hearts onto the four, we will be
stuck, since the four of clubs won't play onto the seven. However, a
clever maneuver will enable us to clear column eight. After reversing
the five-six-seven of
clubs into the empty column 4, move the four of hearts onto the
five! This frees the jack of spades, and we can put the queen of
spades there to regain an empty column. Now reverse the
seven-six-five of clubs into the empty second column (see below).
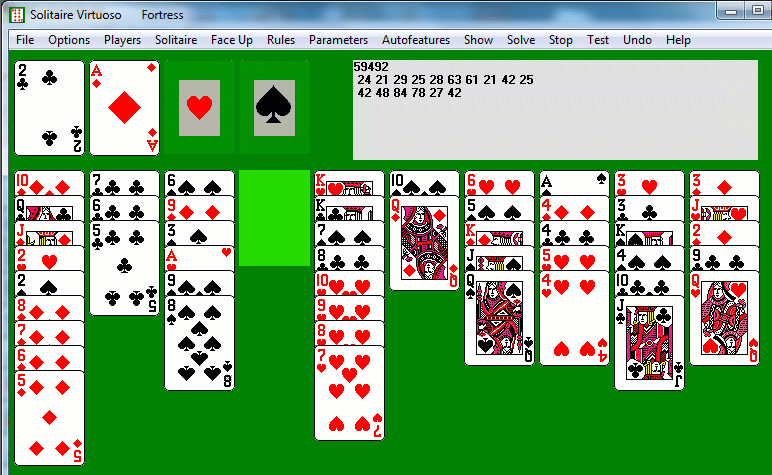
Now the four of clubs has somewhere to go, and reversing the four-five of hearts allows column 8 to clear (four of clubs on five, four of diamonds on five, ace of spades to foundation). If we can get the ace of hearts to the foundation, we can clear all of column 1 (since we can see that after reversing the four-through-eight of diamonds, the twos would go to the foundation and the remaining cards have places to go). But we still only have one empty column, and we need to get the ten of spades uncovered. Reverse the queen-jack of spades, play the queen of diamonds on the king, and the ten of spades on the jack. Now we can reverse the eight-nine of spades and then put them on the ten. Now the ace of hearts goes to the foundation, and we reverse the four-through-eight of diamonds. The twos (and three of spades from column 3) autoplay, then the jack of diamonds goes onto the queen, the queen of clubs onto the jack, and the ten of diamonds on the jack.
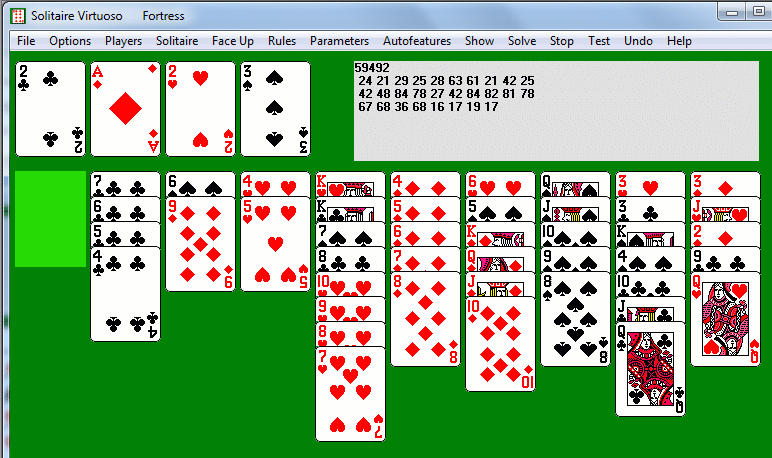
Now the road to victory is open, as we can empty two more columns quickly. Put the nine of diamonds, followed by the ten-through-king, onto the eight, then reverse king-through-four into column 1. Put the five of spades on the six, and the six of hearts (followed by the five-four) on the seven. We plan to clear column 9 next, so reverse the eight-through-queen of spades so that there is somewhere to put the king (this isn't strictly necessary, but it is good technique not to waste columns). Now reverse the queen-jack-ten of clubs (four-five-six of spades autoplay), and put the king of spades on the queen. This autoplays the threes of clubs and hearts, followed by the four-through-ten of hearts and the four-through-eight of clubs. Now reverse the eight-through-king of spades (which autoplay immediately), and then play the queen of hearts to an empty column (strangely, this is the first time we have touched column 10), and everything else autoplays.
The full sequence of moves is:
59492
24 21 29 25 28 63 61 21 42 25
42 48 84 78 27 42 84 82 81 78
67 68 36 68 16 17 19 17 36 76
61 73 75 45 84 96 94 42 A4
This article is copyright © 2008-2021 by Michael Keller. All rights reserved. Most recently edited on October 2, 2022.