Mount Olympus -- a detective story of sorts

Mount Olympus is a two-deck game in which sixteen foundations (all of the aces and twos) are built upwards in suit in alternating ranks (to kings and queens respectively). The original game appears to be German; it appears in "Illustriertes Buch der Patiencen" (published in about 1875). I found the original German rules on Peter Voke's website, which is no longer online. The name there is Der Olymp; it appears under the same name but with English rules in Lady Adelaide Cadogan's "Illustrated Games of Patience" (Second Series, 1887) and later in the 1914 American edition "Lady Cadogan's Illustrated Games of Solitaire or Patience", with identical rules but with the English name Mount Olympus.

I summarize the rules:
Eight aces and eight twos are placed as foundations, and built up by twos in suit (A/3/5/7/9/J/K; 2/4/6/8/T/Q). Nine cards (battery) are dealt as a tableau; packed downwards in suit in alternating ranks (the reverse of the foundations). These cards can be built on each other, moving only one card at a time. Spaces are filled from the stock or waste. The stock is dealt one card at a time, cards being played as possible to the foundations, packed on the tableau, or left on the waste. The waste can be turned and redealt once.

There is no suggestion of a Spider-deal (was such a mechanism even known in the 19th century?) or moving sequences.

But the version Cadogan describes is not found in any later book I have seen, nor any computer implementation. I originally played Mount Olympus, with little success, in computer form in Solitaire's Journey, and later in its successor Mega Solitaire. Instead of dealing the stock one card at a time, the computer versions use a Spider-deal, placing one card on each of the nine tableau piles. Empty piles are filled automatically from the stock. Once the stock is exhausted, empty spaces cannot be filled. This is how the game is described in most modern books: Morehead/Mott-Smith (1949), Moyse (1950), Hervey (1977), Parlett (1979), and Arnold (2002).

Harrod (1997) says that once the stock is exhausted, tableau cards can be moved to empty columns to expose needed cards. The other sources are silent on the point, except Parlett, which says "There is no escape if the game blocks once the stock is exhausted." Harrod, Moyse, and Parlett also allow partial sequences to be moved; Arnold, Hervey and MMS specifically forbid this.

One day I was playing various games in BVS Solitaire and hit Mount Olympus by accident. I won easily; BVS allows tableau spaces to be filled when the stock is empty, as Harrod suggests. So do the versions in Pretty Good Solitaire and Politaire. I started checking sources, eventually finding the references on Peter Voke's site which described a very different game. Where did the Spider deal come from? The only source between Cadogan and Morehead/Mott-Smith in which I have found the game is George A. Bonaventure's 1932 "Two-Pack Games of Solitaire", where the game is described on pages 64-65. Bonaventure allows sequences to be moved as a matter of general policy; did he introduce the Spider deal, or did he get it from some unknown source? And if he did introduce it, why?

Having no computer version of the original available, I got out a double deck and played several deals. Although the waste builds up early in the game before most of the low foundation cards appear, I won easily every time; the redeal of the stock was never necessary; indeed, the waste was usually depleted before I had even dealt out all of the stock. The game is so easy in its original version I wonder who thought that redealing the stock was even needed. Certainly there is no indication that early authors felt that games should be winnable every time.

I implemented a computer version in Dan Reed's Solo package (the limitations of all of the game editors available in various packages is another story for another day), and played several more times, winning on the first deal almost every time. Maybe Bonaventure was on to something -- the original version is almost self-working and too easy to win.

So I found myself back playing the version implemented in BVS and PGS. This version is extremely easy to win, and is probably almost a sure thing with skillful play (PGS and BVS both have top scores on their web site of 100%). You can actually win without even doing any packing of the tableau, just dealing automatically with autoplay turned on, and then managing the empty spaces carefully once the stock is empty (the endgame is sometimes interesting when played this way).

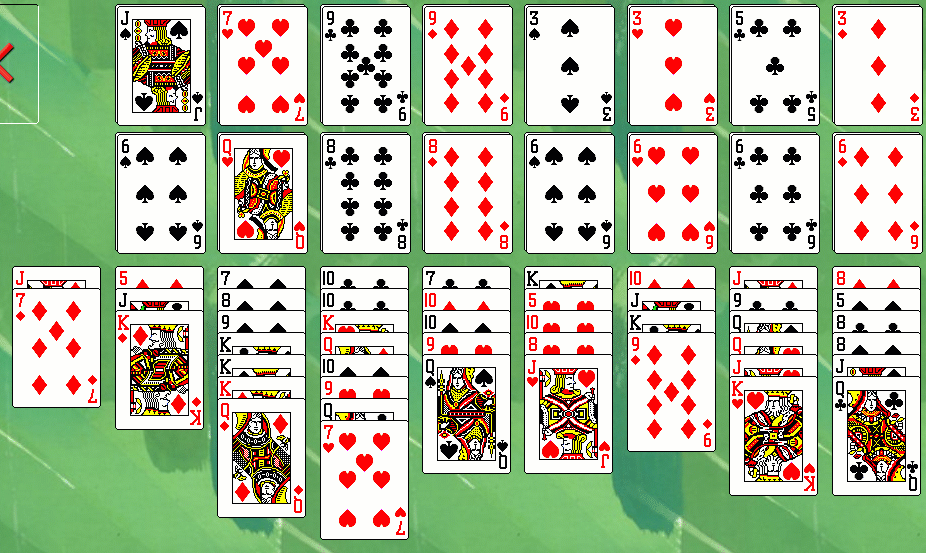
A game of Mount Olympus in progress in BVS Solitaire.   The stock has been fully dealt out, and the endgame is about to begin.   The seven of diamonds goes onto the nine, freeing the jack of diamonds to go to a foundation pile and creating a space.   The game was eventually won.

I won over 80% of the time this way, but was having a hard time ever winning without moving cards to empty spaces at the end.  Morehead and Mott-Smith quote odds of 5 in 6; Parlett says "Odds in favour". After I did win once by accident, I started to see that a different strategy was required. I turned autoplay off (as the wrong card might be selected from two identical available cards), and also realized that it was a bad idea to play a high-ranking card to the foundations too early, especially when it was the last card in a column. I started leaving the high cards in the tableau and use them for packing, and started winning about half the time. I don't know if a skilled player can actually achieve five out of six.

So my conclusion is: the game as originally described is too easy; someone introduced a Spider deal to make the game harder. Most computer implementations found this version too hard, so they changed the rules to allow empty spaces to be filled in the endgame (so that e.g. kings and queens blocking lower cards can be moved out of the way). But the Spider/nofill version (as in Solitaire's Journey, and most current books) is the best; it's the most challenging, requiring the player to think from the very beginning of the deal.

This article is copyright © 2007, 2015, 2021 by Michael Keller.   All rights reserved.    Most recently edited on April 2, 2021.