Maverick Solitaire

An early form of Poker solitaire is actually a puzzle, one which has been called Maverick solitaire (after its appearance on the 1950's/1960's Western T.V. show Maverick, in the first season episode Rope of Cards.  Other shows have also featured the same game).  Twenty five cards are dealt from a shuffled 52-card deck.  The object is to divide the 25 cards into five groups of five cards so that each is a pat hand in draw poker (a hand which does not need to be drawn to).  Maverick Solitaire is well-known as a sucker bet, as the probability of success with a random group of 25 cards would seem low, but is actually quite high: the eponymous author of Maverick's Guide to Poker estimates the odds to be at least 98 percent (he disallows four of a kind).  This is remarkably accurate: Mark Masten's computer solver, allowing four of a kind, solved 98.26 percent of a random set of a million deals.  Deals with unique solutions are even less common than impossible ones: one of Mark's early samples of 1000 deals had 19 impossible deals and only 8 with unique solutions.

The pat hands we need to consider are four of a kind, full house, flush, and straight.  The best place to start in solving a problem in Maverick solitaire is to divide the cards into suits, checking to see which suits have five or more cards, enough to make a flush.   When each suit has five or more cards (which should happen in slightly over 50 percent of deals), it is often possible to make four flushes, and then a fifth hand using the excess cards over five in each suit.  For example, if the suit distribution is 7-6-6-6, any two cards from the long suit and one card from each other suit can be selected in an attempt to make a full house or straight.  A card can be matched in six ways: as part of a flush, as part of a straight, in a pair combined with another three-of-a-kind, in three-of-a-kind combined with another pair, in four-of-a-kind, or as the fifth card added to another four-of-a-kind.   Martin Gardner (see Bibliography) discussed the game and showed an example of an unmatchable card, but such cards are rare.  The most common type of unsolvable deal seems to be a hand with one or two four-card suits, with cards widely spread to make straights difficult.  The renowned mathematican L.E. Dickson (History of the Theory of Numbers) wrote a brief article which was published in Science magazine in 1922, showing an impossible deal with no triplets and three widely-spaced diamonds (see the Bibliography for an online copy).

Here is a deal I found with a unique solution, which was originally published in The Games Cafe of January 27, 2000:



Here's another which was dealt randomly by Solitaire Virtuoso (number 6568):



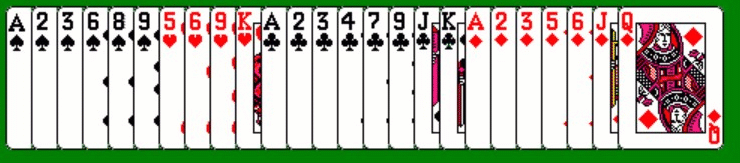
This one was published as a page break (page 26) in WGR13 in February 1998 (the solution has two interchangeable cards):



History
The earliest reference I have is Pope and Johnson's 1928 book 30 Games of Solitaire, where it is called Patience Poker (the book incorrectly states that it is always winnable).   It also appears as Poker Solitaire in the 1939 edition of The Official Rules of Card Games by the U.S. Playing Card Company.   Maverick is not found very often in computer implementations, but there is a version in Solitaire Virtuoso.  Any two cards can be swapped by clicking on them in succession; the program automatically detects when the cards are arranged to that the five cards in each row form a pat hand.  [A dedicated program might allow the player to select difficulty levels, by including a solver, or by selecting various suit patterns (for example 7-6-6-6 for easy deals, 7-7-7-4 for harder ones)].

Four of a Kind
Some sources, like Pope/Johnson and Maverick's Guide to Poker, disallow four of a kind.   This slightly decreases the win rate: Mark Masten's solver found solutions to 97.8% of one million deals with four of a kind disallowed.

Bibliography
Brown, Douglas -- The Key to Solitaire, Ottenheimer, 1966 (later reprinted as 150 Solitaire Games)
   pp. 14-17 describe Maverick under the name Poker Solitaire
Dickson, L. E. -- An Unusual Solitaire Game, Science, New Series, Vol. 56, No. 1450 (Oct. 13, 1922), pp. 418-419
Gardner, Martin -- Mathematical Magic Show, Vintage, 1978, (Knopf, 1977),  ISBN 0-394-72623-5
   Chapter 7, "Playing Cards", pp.94-104
Maverick, Bret -- Maverick's Guide to Poker, Tuttle, 1994, ISBN 0-8048-3032-0
   pp. 131-132 discuss Maverick Poker


Solution to Games Cafe
There are three possible flushes, and no fours-of-a-kind, so the remaining hands must be straights or full houses, which must include all four diamonds.   If there were a club flush, the 6D would be isolated, as it would be the only six remaining, and there would be no 2's or 7's to form a straight.  So the 2C must be part of a straight.  If it were 2-3-4-5-6, the other six would be isolated as before.   So there is one straight of A-2-3-4-5, and the two sixes must be combined with three-of-a-kind.   If the straight contained 5S, the 5C would be isolated, so 5S must be part of a spade flush and A-2-3-4-5 must include AH, 2C, 4D, and 5C.    If there were a  9-T-J-Q-K straight, there would be no threes-of-a-kind left to make a full house with the pair of sixes.  If there were no heart flush, 8H would have to be part of an 8-9-T-J-Q straight, leaving kings as the only triple (which would go with the sixes), but 4H would have to pair with 4S and there would be no way to form a second full house.    So there is a heart flush as well as a spade flush, plus the 2-3-4-5-6 straight and a full house including two sixes.   The fifth hand cannot be a full house, as we would have to include sets of 9, T, Q, and K to use up the leftover clubs and diamonds.   The fifth hand must be a straight including 8H, 9D, TC, and QD, leaving only kings to form a 6-6-K-K-K full house.  There are only five hearts left, which must form a flush 3-4-T-J-Q.   There are seven spades left, so they provide the 3S and JS to finish the two straights.  The unique solution is:
AH 2C 3S 4D 5C     6C 6D KC KH KS    8H 9D TC JS QD    4S 5S 9S TS QS     3H 4H TH JH QH

Solution to Virtuoso 6568
AC 2C 3C 7C JC     AS 2S 3S 6S 8S    AD 5D 6D JD QD    2D 3D 4C 5H 6H    9S 9H 9C KH KC

Solution to WGR13
2S 2H 2D KS KD    3D 4S 5D 6C 7S     7C 8H 9C TC JC    AH 4H 5H TH QH    AD 6D 9D JD QD   (7C / 7S interchangeable)


Copyright ©2024 by Michael Keller. All rights reserved.  This file was revised on May 9, 2024.