Shamrocks: another detective story
by Michael Keller and Mark Masten

One of the games which appears in William B. Dick's 1883 book Games of Patience is a game which he calls The Shamrocks, listed as a variant of La Belle Lucie (though it resembles it only slightly).  Unlike La Belle Lucie, Shamrocks is a completely open game: there is no redeal.   This is a one deck game in which the cards are dealt into seventeen packets (fans in the usual terminology) of three cards each, with the last card forming its own packet.   The object is to free up aces and build them in suits to kings as usual.   Fans may be packed downward, regardless of suit, but no fan may contain more than three cards.  This means that the only plays possible initially are playing any available aces (and subsequent cards) to the foundations, or packing an available card onto the single card.    No card may be moved to an empty column.  Dick allows the player to move any king which is covering a card of the same suit in its fan to just below the card it covers (as in Nestor, we'll call this process of fixing a deal rectification).   In the deal below, Dick would rectify by moving the KS to the bottom of the 14th column, below the AS.    The game appeared again in 1890 in Cavendish's classic Patience Games, under the title The Three-Card Fan.   The rules are the same, except that Cavendish rectifies more aggressively, putting kings at the bottom of their fans (he calls them depots).  In the deal below, the KS and KD would both go to the bottom of column 14, presumably with the KD at the bottom since it was dealt last.   In addition, Cavendish allows any extra kings in a column to fill empty spaces once uncovered.  In the position shown, once the AS is played, the KS (second in the column) could be played to an empty column as soon as one appeared.   Cavendish plays through a full deal, and also a composed problem with a partly completed deal (these are both rather bland).   He claims the odds are slightly in the player's favor with best play.

George A. Bonaventure's 1931 Games of Solitaire drops the article and simply calls it Shamrocks: he follows Dick's rules, as do subsequent books up through Coops in 1939 and Moyse in 1950.   The exception is Morehead and Mott-Smith's 1949 classic The Complete Book of Solitaire and Patience Games, which allows packing upwards or downwards (or both) on any column: in the position below either available five could be played on the 4S, and another four (or a six later) on the five.  I do not know if this rule was one of Morehead and Mott-Smith's many innovations: they do not say so.    Morehead and Mott-Smith estimate the odds of winning as 1 in 4, and suggest that if there are no initial plays, any covered ace be allowed to be drawn out to start a foundation.   Virtually all recent books and computer implementations follow Morehead and Mott-Smith in allowing packing in both directions: BVS Solitaire has a fine implementation, in which deals are not rectified.   David Parlett's 1979 classic Penguin Book of Patience Games is the only source which mentions both versions: he uses Three-Card Fan as the name for the downward-only version.    [We suggest the name Classical Shamrocks for the original version with downward packing only, and Modern Shamrocks for the version with packing in both directions.]

Several sources point out that no deal can be winnable unless the bottom row (first dealt) has at least one king in it.  Mark Masten proved this easily by pointing out that the last card played to the foundations must be a king, and kings are not allowed to move to empty spaces (except in Cavendish's variant, which already has kings at the bottom of their columns).    Deals with no kings in the bottom row occur about 17% of the time in unrectified deals.   (The exact same odds apply to deals with no aces available at the start.)   If deals are not rectified, it is reasonable to add a grace to the standard rules, allowing the player to move one available king to an empty space, at any time during a deal in which no kings were dealt to the bottom row.



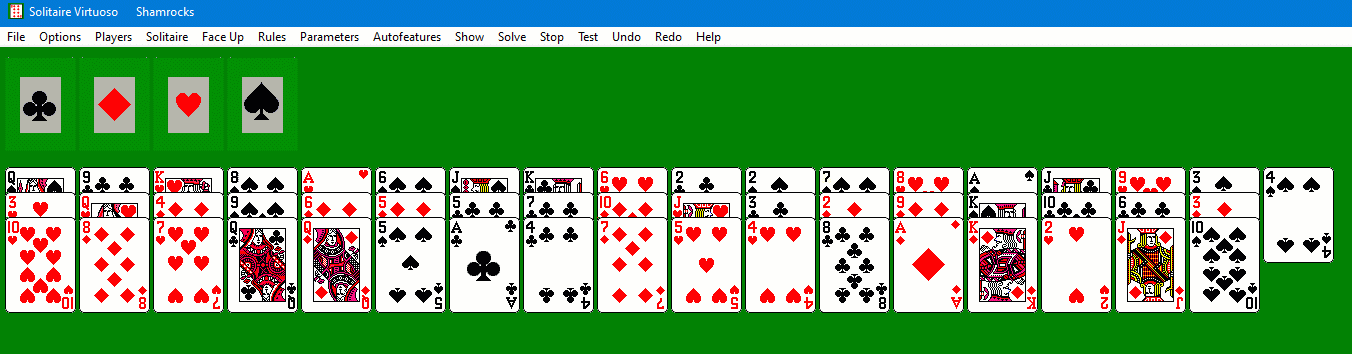
A sample deal of Shamrocks, number 78814 in Solitaire Virtuoso.   Under the original rules the only playable cards are the two uncovered aces.  This frees 5C and 9D for further plays.   Under the modern rules any available five may be played on the 4S. 

When Mark Masten told me he was working on a solver, I implemented Shamrocks in Solitaire Virtuoso, and as usual simply dealt 18 columns, making it easy to see which columns have space.   I had forgotten that the rules allow for rectification of the kings, so I dealt it entirely randomly (row by row, rather than each column as the original rules specified).  A little over 1% of deals will be completely blocked at the start, having no aces and no card to play on the single card.   I played quite a few games and won a little less than half.   I was playing by modern rules, which allow cards to be packed both upwards and downwards: either available five may be played onto the lone 4S.   This produces much richer play in my view, like a very limited version of Fortress.  

Let's play through the deal above.  Start by playing AC and AD to start two of the foundations, then 4C onto 5C and 8C onto 7C (packing upwards) to free the 2D, and the TS onto the 9D to free the 3D.   Next reverse the 8C and 7C onto the 7S, and the QD onto the KC.  Next the 5H and 6D go onto the 4S, freeing the AH to start a third foundation.  That column is now empty, and out of play for the rest of the deal.   The 2H follows the AH, and the TH goes onto the JH, and two more hearts (3H, 4H) can go to the foundations.  JD and TH go onto QS, and JH onto QD, freeing 2C and 3C for the foundations.   (This is a common maneuver, using two columns to split a two card sequence).   It actually looks pretty bad at this point (see below): although three foundations are under way, we have lost two columns already and two more are down to low cards.  It looks like there's not much room to maneuver.



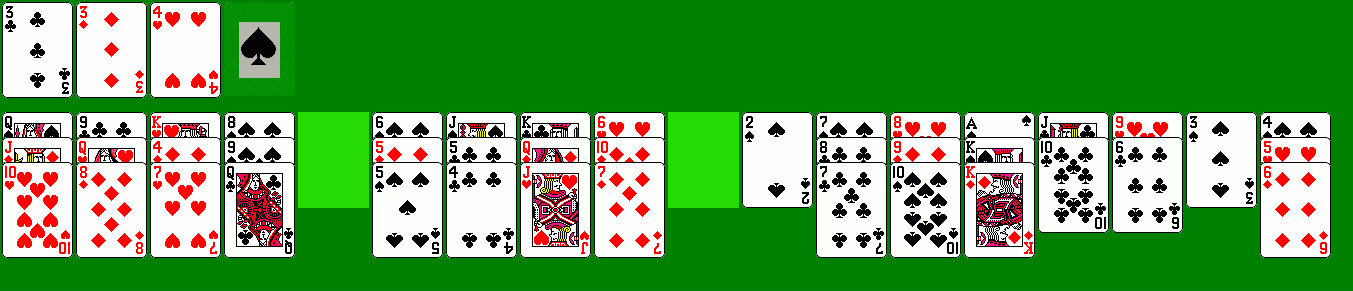
Now reverse the 4C and 5C onto the 3S, and the QC and KD go onto the JS.   7H goes onto 6C, freeing 4D for the foundation.    Now JH goes onto TC.   It would be a disaster here to move KS onto QD and start the last foundation with AS and 2S, as you would quickly run out of space.   Instead QD and KD go onto KH, and QC and KS go onto KC.  You still shouldn't play the spades to the foundations yet.  TS and 9S go onto JS (usually good policy to build sequences in suit when you can), 9D onto 8S, 7D and 6D onto 8H, and finally send 5H to the foundations.  The goal of this long maneuver was to free up red cards to send to the foundations and make more space in the tableau.  5S goes onto 4S, freeing 5D to go to the foundations and leaving 6S as a convenient base for reversing low cards. 



5C goes onto 6S, freeing 4C, which goes to the foundation followed by 5C.  5S goes onto 4S, getting all of the low spades ready, and now you can send a flood of cards home: 6 through ten of diamonds, 6 through 8 of hearts, 6 through 8 of clubs, 9 through queen of hearts, and jack of diamonds.  All 13 spades can now be sent in sequence, but if you send all of the clubs home you will be stuck.   Instead play the KD onto QC, then both diamonds, the last heart, and the remaining clubs play.



Above is another typical endplay situation, from deal number 78816.   All of the sequences are in reverse order, except for the KQK in column 2.  This can be won by playing TH onto JC, sending 9H and TH home, then playing QD onto JC and sending JH home.  Next KH goes onto QD, finishing the hearts, and KS onto QD, finishing the spades.   QD goes onto JD, followed by KC, finishing the clubs.   Finally QD goes onto KD and the diamonds run, completing the win.


Copyright ©2022 by Michael Keller. All rights reserved.  This file was revised on October 1, 2022.