Whitehead and Agnes -- Packing in Color
Some time after Klondike began to be popular, variations of the
game started to emerge. Two notable variations of Klondike, Whitehead and Agnes,
share several common features:
(1) The entire 28-card tableau is dealt as in Klondike, in seven columns of increasing length, but all cards are dealt face
up.
(2) The tableau is packed in color rather than in alternate colors
(i.e., the six of hearts can be packed on either the seven of hearts or
the seven of diamonds). Both games also allow sequences of cards to be moved
as a unit, but only if they are in the same suit:
6H/7H/8H can be moved together (and packed on either red 9), but
6H/7D/8H cannot be moved together.
(3) The foundations are built upwards in suit from a random rank
determined by the 29th card dealt, which becomes the first foundation
base. Unless the foundation base is an ace, the ranks wrap around, so that aces are built on kings in the foundation, kings can be
packed on aces of the same color in the tableau, and a sequence like QD/KD/AD/2D can be moved as a unit.
(4) Empty columns can be filled with any available card or in-suit build.
Let's look at Whitehead
first, which was invented by the noted bridge player and author Wilbur
C. Whitehead (and obviously named after him). It was
already an established game by 1924, when it appeared in the 28th
edition of The Official Rules of Card Games
by the U.S. Playing Card Company. Several other books in the
1920's and 1930's included it, but somewhere along the line someone
left out the random base, and most modern sources (including every computer
program I have seen) build the foundations from aces. David Parlett's The Penguin Book of Patience
is the only recent source which uses Whitehead's original rules.
It is a very fine game, with odds in the player's favor with skillful
play (the prefounded base gives the player a slight head start in
building foundations).
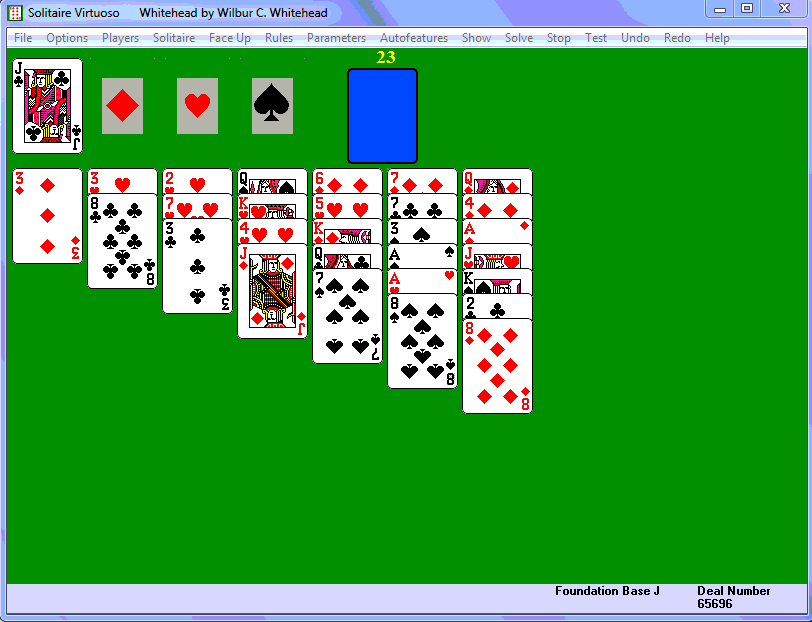
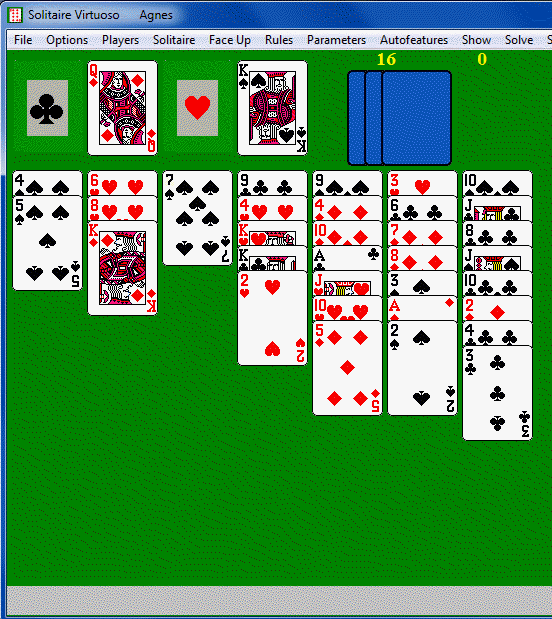
Here is a sample deal from Solitaire Virtuoso
(click the link to get the full sequence if you want to follow with a
deck of cards). The foundation base is a jack, so the JD can
immediately start the diamond foundation. The 7S can be packed on
either the 8C or the 8S: the latter is preferable so that 7S/8S can be
moved together. The 3D is then packed on the 4H, which leaves an
empty column. Any available card or sequence packed in suit can
be moved to an empty column. In this case we move 3C to the
empty column, pack 7H on 8D, and 2H on 3D. We have an empty
column again, but it is not necessary to fill it immediately. The
game now proceeds like standard Klondike, dealing the stock one card at
a time to the waste, making any available plays the player chooses
before dealing the next stock card. The top card of the
waste is always available. In this case we deal the first
stock card, a 4C. This gives us an easy play, putting it in
the empty column 3 and packing 3C on it, still maintaining one empty
column. The next stock card is KC, which plays directly to
the club foundation. The next stock card 2S could pack on 3C, but
we plan to eventually pack 3C/4C onto column 6 to free up another
space. The next stock is 6S, which packs onto 7S. As soon
as we get a black 5, we can pack it there and follow with the
3C/4C. It's not ideal to have long color sequences with
mixed suits, but eventually we may be able to untangle them. 9H
and TD follow from the stock, then we get the 5C, which packs on 6S,
followed by the 3C/4C. The current position is shown below
left.

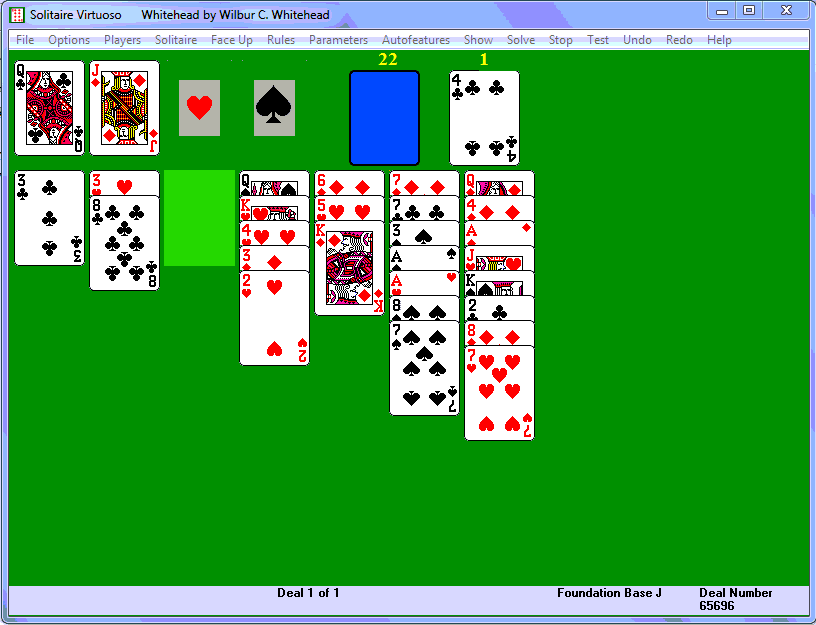
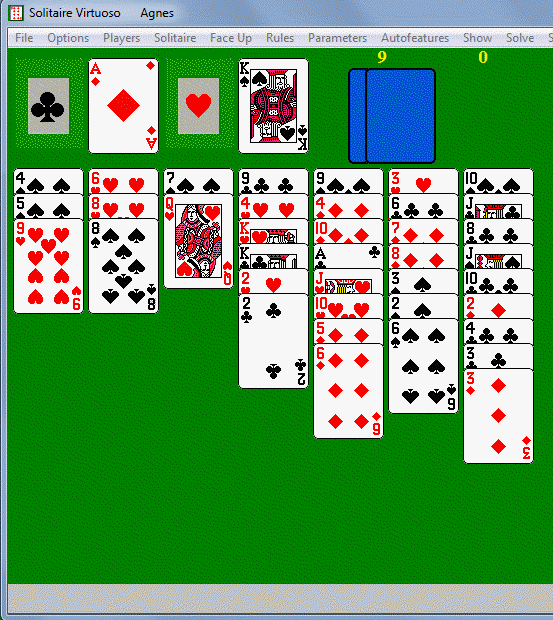
At this point we decide to play the 7H and 8D from column seven,
placing the 7H in column 3, 8D in column 1, then packing 7H on
8D. The 2C packs on 3C, and putting KS in column 3 sends the JH
to start the third foundation. Now a series of plays frees up the
QD: AD on 2H, KD on AD, 4D on 5H, and the QD, KD, and AD go to the
diamond foundation. We can get another empty column by playing 8C
to column 7 and then consolidating the low diamonds somewhat: 2H on 3H,
3D on 4D, 2H/3H on 4H. (We're trying to make maneuvers to
decrease the disorder in the red and black sequences without giving up
any spaces.). The next stock cards are 9S and 4S, followed
by the JS, which starts a third foundation. We're hoping for the QH,
which will let us move 2H/3H/4H to the empty column and build KH, QS,
and KS. Next follow a series of stock cards that don't help
us: TC, 5S, 5D, TS, 6C, and TH. The 9C comes up and we can
play it in the empty column and pack 8C. Then comes 9D,
and finally QH. We do as we planned, giving us two empty
columns (above right). We put the clubs from column 6 into
column 4 and the spades into column 3, which lets four hearts and the
AS go to the foundations. We play the last four stock cards,
ending with the AC, which plays five more clubs. We can
easily backtrack through the waste, packing and consolidating as
needed, to finish the game.
Mark Masten has adapted a solver for Agnes, written by Jan Wolter and
posted on Politaire, to analyze the win rate for Whitehead, using thoughtful play (the solver knows in what order the stock is dealt). Under the correct rules, with one base prefounded, the solver
played 100,000 games of Whitehead and won 91,177, so the upper bound on the win rate is just over 91%. A
human player can only hope to reach this by using undos or replaying
the deal, perhaps multiple times (some players do this). The
common incorrect version, building from aces with no cards prefounded,
is only slightly harder; the solver won 9,025 out of a smaller sample
of 10,000 deals.
The confusing tale of Agnes
The first appearance of the variant game Agnes appears to be in Ernest Bergholt's A New Book of Patience Games
(the first
of his two volumes on card solitaire), which was first published about
1915. Bergholt says: "This is a good but difficult game,
which has not been published in any previous book, though it has been
known and practised for at least the last five or six
years." Probably it is a slightly older game than
Whitehead; whether Wilbur C. Whitehead was aware of Agnes is
unknown. It actually starts out the same way as Whitehead,
with identical tableau, foundation base, and rules for packing and
moving sequences. Where Agnes diverges from Whitehead is in
the stock deal. Instead of dealing one by one, Agnes uses the
same deal as Spider: one card is dealt to the bottom of each
column. After each set of seven cards is dealt, the player may
make any available building and packing plays. Bergholt is explicit that an empty column can
be filled by an available card or packed sequence of one suit; it can
also be left vacant until the next spider deal. There will be two
cards left over; the player may look at these before making plays on
the last full set of seven; they will eventually be dealt to the first
two columns (Parlett's interpretation). Bergholt says "these may
be at once looked at, in order to save time." (it's not clear to me
what that means). Bergholt gives a sample deal played through,
and
estimates the win rate at 1 in 6 or 7 deals. Basil Dalton quotes
that figure in his first volume, Games of patience: fifty selected games for a single pack,
which first appeared in 1924. He gives essentially the same rules
as Bergholt, and likewise plays out a sample deal. Accounts of
the game with Bergholt's rules appear in books by Bonaventure and
Hervey, among others. This should be considered the
standard version of Agnes, but things later started going haywire, as
usual. The rule for filling spaces got muddled: depending
on the source, spaces could only be filled by a single card (implied by
Dalton but perhaps misstated), not until after the first spider deal (Johnstone), only with
a card of rank one less than the the foundation base, or not at all.
The rules for movement also got muddled: some sources allowed
packed sequences of one color to be moved as a unit even if suits were
mixed (all of the computer versions I have seen allow mixed-suit groups of the same color to be moved).
Mark Masten has also analyzed a number of rules variants
using the
same
modified Politaire solver used to analyze Whitehead. In
standard
Agnes, as described by Bergholt, the solver, again with thoughtful
play, won 63,635 games out of a sample of 100,000 deals, so the win
rate can be over 63% if a deal is replayed enough times.
When empty
columns are not allowed to be filled between spider deals, the win rate
drops calamitously to less than 1 percent (96 wins out of a smaller
sample of 10,000). With columns allowed to be filled, but only with the rank one less
than the foundation base (or a suit sequence starting with it), there
were 1,424 wins out of 10,000 (slightly above 14%).
I wish this were the end of the sad story. Unfortunately, a
completely different version of Agnes branched off, which is much
closer to Klondike. It has the same tableau and foundation base,
but packs the tableau in alternate colors as usual. Packed
sequences in alternate colors can move as a unit, and empty columns can
be filled with a card of rank one less than the base, or a packed
sequence starting with that card.(e.g. a six if the foundation base is
a seven). There is also a seven-column reserve, which starts with
one card in each column. Now the spider deal isn't to the
main tableau, but to the reserve. Uncovered reserve cards are
freely available for building or packing (on the main tableau columns, not each other). This version
seems to have popped up in American books in the 1930's and 1940's, such as Helen L. Coops' 1939 compendium 100 Games of Solitaire: by
the time it reached Morehead, Mott-Smith, and Moyse, it wasn't even an
open tableau any more: in their books the tableau is closed like
standard Klondike. David Parlett, aware of two very
different games, named the original Bergholt version Agnes Sorel
(though he has the no-fill rules), and the Klondikesque version Agnes
Bernauer. The names don't help much, considering how much the
rules for both versions have splintered. Agnes Bernauer (the original open version) is a very
playable variant, with a higher win rate than standard Agnes: the thoughtful solver won 8,857 out of 10,000 deals.
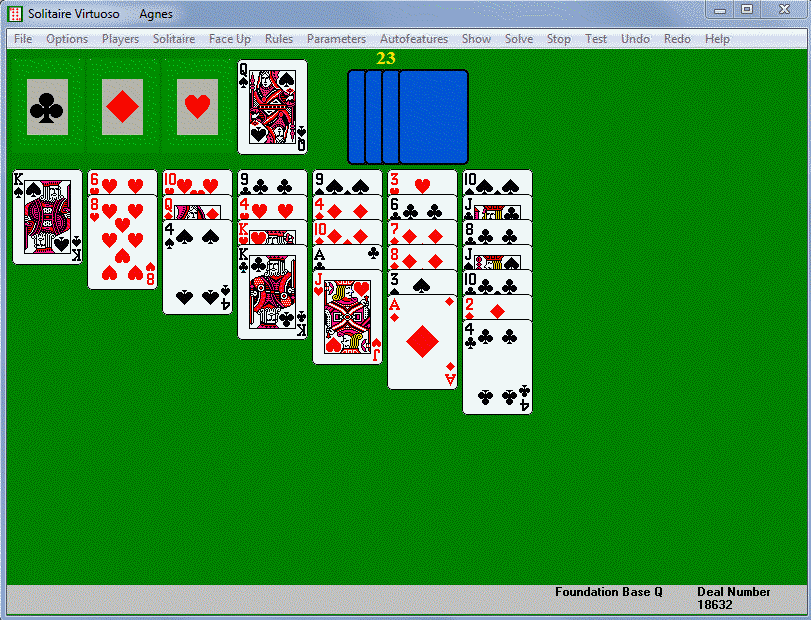
But let's return to Bergholt's original rules and see a sample
deal of Agnes. Remember that we pack in color, move groups only
if they are all the same suit, and can fill empty columns with any
uncovered card or in-suit group. In this game, unlike Whitehead,
we don't care much about keeping spaces, because they will be filled in
on each spider deal. The KS plays immediately to the QS
foundation base, and we can free the QD to start the second foundation
by playing 4S to the empty first column. After QD goes, we pack
TH on JH. With no obvious plays, we leave the third column
open and deal the first seven cards from the stock (above right).
The KD plays to the foundation, and we can pack 2S on 3C to free the
AD. We then repack 2S on 3S to form a unit in suit, and deal
again (lower left). QH starts the third foundation, then we pack 7S on
8S, 6S on 7S, and then move 9S to the empty column and pack 5S and then
4S on 6S. Now we move the 2S/3S as a unit and pack it on
4S. We reverse the 8D and 7D into column 1, following with 6D and
5D. Now 9H packs on TH. It seems reasonable now to fill the
space with 9H/TH/JH and packing AC on 2C, before dealing the next seven
cards (below right):
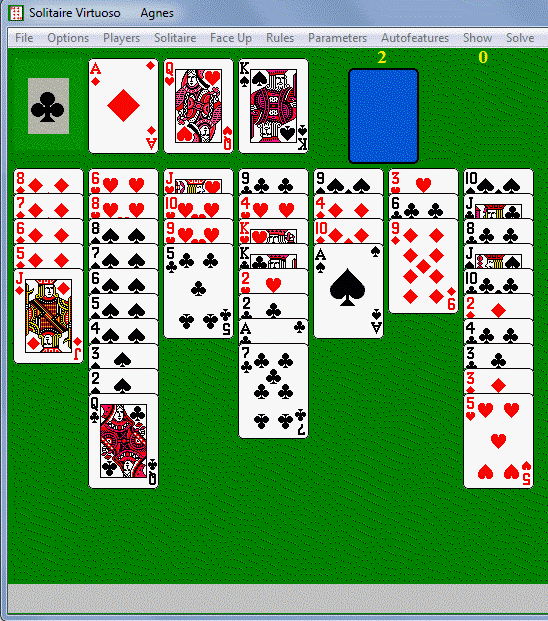
The QC starts the last foundation, and AS and the 2S-8S sequence
go to the spade foundation. TD and 9D pack on the JD, followed by 6C
and 5C on the 7C. 8H packs on 9H, 5H on 6H, 3D on 4D, and 3C/4C on
5C. 2C through 4C now go up, followed by 9S which frees an empty
column and makes the rest plain sailing. 9D/TD/JD go to column 3,
and all of the diamonds build. 3C-7C go to either empty column,
followed by AC/2C, and 2H packs on 3H. Now KC and AC-7C build,
followed by KH. 4H and 2H/3H pack on 5H, we put TC and JS in
empty columns, building the rest of the clubs and spades.
There are only hearts left, and the missing AH and 7H are the last two
cards, which run the hearts and win the game.
The original Agnes is a decent game (though Whitehead is preferable for
me): although some deals block quickly, the deals where there are
packing plays available on the initial deal produce interesting play
(somewhat like Fortress in that regard).
Sample deal 65696 [Note: Solitaire Virtuoso deals the random base before dealing the tableau):
JC 3D 3H 2H QS 6D 7D QD 8C 7H KH 5H 7C 4D 3C 4H KD 3S AD JD QC AS JH 7S
AH KS 8S 2C 8D 4C KC 2S 6S 9H TD 5C 9S 4S JS TC 5S 5D TS 6C TH 9C 9D QH
2D 8H 6H AC
Sample deal 18632
QS KS 6H TH 9C 9S 3H TS 8H QD 4H 4D 6C JC 4S KH TD 7D 8C KC AC 8D JS JH
3S TC AD 2D 4C 5S KD 7S 2H 5D 2S 3C 9H 8S QH 2C 6D 6S 3D JD QC 5C 7C AS
9D 5H AH 7H
Most recently edited on May 14, 2021.
This article is copyright
©2021 by Michael Keller. All rights reserved.







