Nestor and Double Nestor --
Rank Pair Discarding Games
by Michael Keller and Mark Masten
One of the standard single-deck open games is Nestor, probably
named after a
mythological Greek king, one of the Argonauts. The game dates back at
least to the German book Illustrirtes
Buch der Patiencen,
first published in 1877, and later translated
into other languages including English. (It's also one of a
handful of very early games to be named without a definite
article). It is
called Matrimony in some older books (e.g. New Games of Patience
(1911) by
Mary Whitmore Jones), an unfortunate name which has been applied to
other games. Nestor is the most common of the family
of rank pair discarding games. In the standard one-deck version, the
deck is dealt out row-by-row into a tableau of eight columns and six
rows. The remaining four cards are dealt face up below the
tableau columns as an open reserve. The uncovered card in each
column, as well as the four cards of the reserve, are available at any
time. Cards are discarded in pairs of the same rank; each
discard uncovers new cards in the tableau. The object is to
discard all 52 cards in pairs of the same rank. [Some
older sources specify that the last four cards are dealt as a
closed reserve, in which the four cards can be only be used in order,
which is unnecessarily harsh and adds nothing to the strategy of the
game.]

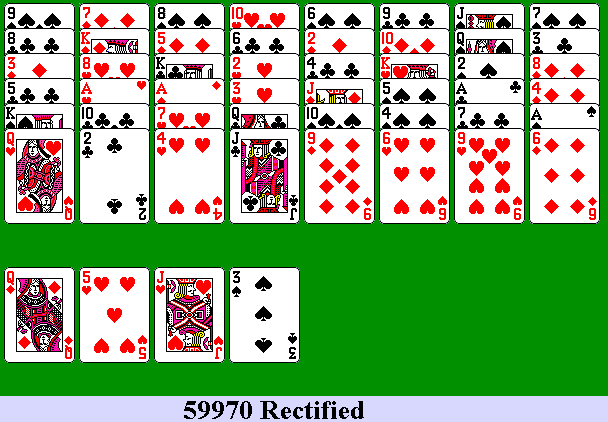
Above left: an unrectified deal of
Nestor, number 59970 in Solitaire Virtuoso. Note that six
of the eight rows contain repeated ranks. Above right: how
the deal comes out when rectified. Both versions are winnable.
If the cards were dealt randomly, the game would become very
difficult (with a win rate less than 1 out of 7, according to Mark
Masten's computer analysis of 100,000 sample deals, reported to the
Card Solitaire Forum mailing list in 1999). The reason for this is
that cards of the same rank tend to be to be dealt to the same
column. Somewhere around 40% of deals would be impossible
by inspection because they have three of the same rank in the same
column. The standard procedure for dealing, which I call rectification,
is to deal row by
row, placing on the bottom of the deck any card which would duplicate
ranks in the same column. The last four cards (almost always would-be
duplicates) then become the
reserve, which may contain duplicate ranks. This is how the game
is invariably described in print; careless computer adaptations
sometimes leave out the rectification. Dealt in the
standard way, the game has a win rate of just above 4 in 7 with
perfect play. [The standard rectification scheme
fails on rare occasions; the easiest way to handle it is probably just
to reshuffle.] The Nestor family of variants are quite
difficult: human players should expect to fall far short of the
theoretical win rates calculated by Mark Masten.
A reasonable rule to follow in unrectified versions of Nestor is to allow overlap discards:
two cards of the same rank in the same column can be removed together
if one is uncovered and directly covers the other. In the unrectified version of 59970 above, four pairs can be
removed under the overlap discard rule once all the cards above them are
removed: 9's in column 1, 3's in column 3, 6's in column 5, and 2's in
column 7. (We also look at overlap discards in the Pyramid article).
Variations of Nestor
You can make Nestor as hard or as easy as you like by
changing the number of columns: Vertical,
a game found in some older books (and which is sometimes confused with
Nestor itself),
has one fewer column of cards in the tableau: seven columns of six
cards each, with ten reserve cards. Sometimes an extra card is dealt to
the center (fourth) column, and only nine cards to the reserve. BVS Solitaire includes two unrectified versions without reserves: Turkish Kerchief deals the entire deck into 10 columns (the first two get an extra card); Full Parade is 9 columns (seven get an extra card). These games come from the 1998 book Pasiasny
(in Russian) by N.IU. Rozaliev. Both games specifically
allow overlap discards, but are nevertheless quite difficult to win. Mark gives theoretical win rates of about 38% for Turkish Kerchief and 13% for Full Parade. Pretty Good Solitaire includes a
variant called Heracles, which
is nine rectified columns of five cards with seven reserve cards, and Alcides, which is ten unrectified columns of five cards and two reserve cards. Heracles has a win rate of well over 99%, but Mark suggests humans should win less than half (PGS estimates 50%); Alcides has a theoretical win rate
of about 45% (Mark expects players will win about 1 in 5; the PGS help
suggests 1 in 4). Neither Heracles nor Alcides permit
overlap discards.
Doublets is a
traditional closed version of Nestor, with only the last card in each tableau
column dealt face up (cards are turned up as they are uncovered).
Doublets is usually dealt to a tableau of 12 columns of four cards each
(non-rectified). The last four cards are a closed stock, which is
used to fill empty columns -- when the last card in a column is
discarded, deal the top card of the stock face up to replace
it.
This makes the reserve less useful than in standard Nestor, as the four
cards cannot be used until you start clearing columns, and a critical
card may not be available at the right moment.
Mark Masten's solver found that the win rate in standard Closed
Nestor, eight columns of six, but with a normal open reserve, is about
1 in 4 if the deals are rectified.]
An interesting version of Nestor is to add jokers to the
deck. An available joker can be matched with any card (though
the second joker must then be matched with a card of the same rank as
the first if all of the cards are to be discarded). This was
first suggested by Walter B. Gibson in his excellent 1964 book How To
Win At Solitaire (where Nestor again appears as
Matrimony). He suggests
just adding the two jokers to the reserve. But Mark
suggests just shuffling them into the deck as usual, and dealing a
six-card reserve with the usual rectification. His variation Nestor's Revenge
has no reserve at all, just nine rectified columns of six cards each,
with two jokers shuffled in randomly. His solver won about 1 deal
in 6.
Double Nestor
There seems to be a widespread idea, which I don't entirely
agree with, that any good single-deck solitaire can be made into a good
double-deck game (this idea is more persistent in computer solitaire
packages; two-deck games which have appeared in the literature are more
likely to have stood the test of time). For a long while, Nestor, however, did not
appear to have been tried as a double-deck game (not counting Mah Jong solitaires). I originally
experimented with this using the game editor in Solitaire Antics
Ultimate, trying out various layouts for a two-deck Nestor. What
I was aiming for is a game which can be won most of the time, but
provides challenging play, particularly towards the end of the game. My
first attempt was 12 columns of 8 (rectified), with eight reserve
cards. This seemed too easy, so I tried 10 columns of 10, with four
reserves. I only won one out of five tries, though that might have been
due to poor play (later I won three out of seven). I then tried 11
columns of 9, with five reserves. I won eight of ten, but it was not as
challenging as I would like -- the winnable deals seem on the easy
side. I have also tried a non-rectified
deal of 12 columns of 8 -- this would be the most consistent with the
original Nestor, and easier to deal by hand, but I won every try and it
also didn't seem hard enough.
In 2003 I asked the members of the Card Solitaire Forum for help,
and
Mark Masten wrote a new solver to handle double-deck variants of
Nestor. He found that rectification got harder as the columns got
longer. It appears that 10 columns of 10 is a very good game,
even without rectification. His solver won about 92 percent
of the time. One interesting version he devised is 7
columns of 13 cards, with rectification, and a 13 card reserve: each
column will contain one of each rank, as will the reserve. I have included the 10x10 unrectified game as
one of the standard games in Solitaire
Virtuoso.
I like this even more than regular Nestor,
though I am still not good at it yet. BVS Solitaire also
included 10x10 unrectified as Double Nestor. Pretty Good
Solitaire adopted 12x8 unrectified for its version of Double Nestor.
In recent years, versions of closed Nestor with multiple decks of cards, using long piles of cards
with only the top card face up, have become commonplace in commercial
packages of thematic solitaire. Sometimes the piles branch off into subpiles, both
branches blocked by a single card. Nestor now trails only Golf as the dominant
mechanism in campaign solitaires.
Basic Strategy


The primary strategic idea in Nestor is to locate potential blocks and
work out a sequence of moves to avoid them. In the sample
deal above left (from WGR12, p.35), there is a simple reversal of ranks
(king and three) in columns 3 and 8, and a more complex tangle of ranks
(four, ace, ten, jack, and five) in columns 1, 2, 4, and 7.
You will need to reach the problem areas quickly before using up the
cards you need to unblock. We show actual discards made in
boldface. Start by discarding the tens of hearts and clubs and the eights of hearts and clubs. Next is the nines of diamonds and clubs, freeing up the kings of hearts and diamonds
(they are blocking two of the critical columns, and there is little
hope of saving one for the king of clubs in column 8. Our
plan is to eventually discard the black threes and then the black
kings, saving the three of diamonds in the reserve for the three of
hearts.) Now the queens of clubs and diamonds and the jacks of clubs and hearts are discarded. The simplest path forward is to discard the black fives, all four sixes, the fours of hearts and clubs, and all four sevens. Now we can discard the black threes and the remaining queens and kings.
We just have to be careful to unblock the ace-four reversal in columns
1 and 2: discarding the black aces here would lose. Instead
we work to free up the four of spades, by discarding the black twos (one from the reserve) and the remaining eights, then the aces of diamonds and clubs, and at last the remaining fours. The rest of the cards come off easily; there is no way to be blocked from this point.
The deal above right appeared in The Games Cafe on April 13,
2000. It is full of potential pitfalls: there is a six-jack
reversal in columns 1 and 3, and an eight-queen reversal in columns 6
and 8. There is also the danger of running out of moves
early, which will happen if you start by discarding the threes of clubs and diamonds will cause you to run out of moves quickly.
You must remove the kings of clubs and hearts, followed by the aces
of spades and diamonds. The first roadblock in this deal is to
uncover another four so that the four of hearts can be removed. Normally you
should not use the reserve cards too soon, but here it is the only way to get at a four:
remove the queens of spades and hearts, then the twos of hearts
and clubs. Now you can remove the red threes and red eights,
freeing the four of spades. (Generally, given a choice between
multiple cards of a rank, you want to discard those from the columns
with more cards, and in fact discarding the eight of hearts
with the eight of clubs would lose because of the eight-queen
reversal.) Now remove the fours of hearts and spades,
and the kings of spades and diamonds
(it is always completely safe to remove the last two cards of a given
rank; this cannot lose unless you were already blocked). You
might want to remove the
two uncovered sixes at this point, but you won't be able to discard the
jack of diamonds
safely if you do (removing the jacks of diamonds and clubs will block
the remaining sixes
and jacks, as we saw at the start). You need to use another
reserve card,
discarding the tens of diamonds and spades, then the red sixes. Now you can remove the jacks of spades and
diamonds, and the sevens of hearts and spades (this is a safe
play since you have a seven in the reserve to take off the seven of clubs).
Next discard the remaining queens, threes, and eights.
It's essential to remove the five of clubs, but removing it with the five of diamonds will
block the remaining fives and aces. Instead discard the fives of clubs and
hearts. The rest is not difficult: the remaining sevens (one from the reserve),
jacks, sixes, and black nines (nine of diamonds would work the same as nine of spades -- a
lone card in a column is the same as a reserve card). The rest come off easily.
Mah Jong
A form of computer solitaire using a set of 144 Mah Jong tiles instead
of playing cards was first developed for the PLATO system in 1981 by
Brodie Lockard. The tiles are arranged in one of a number of
three-dimensional patterns (most notably a pattern called the Turtle)
where many of the tiles are hidden. The object is to remove the
tiles in identical pairs; it is essentially a closed version of
Nestor. Since then hundreds of versions have been published
under various names on every platform imaginable, including many online
versions. The game has been analyzed by Michiel de Bondt.
There is also a similar game called Shisen-Sho (or Four Rivers) where
the pattern is a flat rectangle, but the choice of tiles is restricted
to pairs connected by a path with no more than two right-angle turns.
Copyright ©2024 by Michael
Keller.
All rights reserved. This file was revised on May 6, 2024.



