Beeswax and Beehive -- Building in Ranks

There are only a handful of solitaires in which cards are packed on the tableau by rank.  In a couple of these, packing by rank is only a means to an end. David Parlett's ingenious Curds and Whey is essentially a one-deck relative of Spider; it allows packing on the tableau in rank, and also downward in suit; the object being to form four complete suites (sequences running from king down to ace in suit).   Steve Meretzky's Barbershop Quintet uses packing by rank to facilitate discarding in sequence as in Golf.   In the two games we describe in this article, cards are packed on the tableau in rank only, the object being to form thirteen sets of four.  Beeswax and Beehive are both available in Solitaire Virtuoso.

Beeswax is the name I am now using for an excellent open solitaire I have never seen in a book, though there are a fair number of computer versions.  Among the computer versions still available are Maurice Abraham's Patience Pack (where it is called Pile Sort), a freeware package of 120 games and puzzles first published in 1994 (the current version 8.0, written in 2005, still runs under Windows 7).  The Linux solitaire collection AisleRiot implements it as Pileon.  Pretty Good Solitaire calls the game Fifteen Puzzle: not a particularly good name, as this solitaire is unrelated to the well-known sliding block puzzle popularized by Sam Loyd (fifteen numbered pieces in a 4x4 grid, which have to be arranged in order by sliding blocks into the one space in the grid).

In Beeswax, the entire deck is dealt out in a tableau of 13 columns of 4 cards each, with two empty columns.  It is usually presented as thirteen fans of four cards each, with two empty spaces, the fans and spaces being arranged in a 3x5 or 4x4 array.   I am not a fan of fans: I prefer to have 15 parallel columns, so that it is easy to see which columns have room left.  In Beeswax a card may only be moved onto a card of the same rank, or into an empty column.  Each column can hold a maximum of four cards, so the first play must be to one of the two empty columns.   The object is to form thirteen quartets of the same rank; completed quartets are not discarded.   Suits do not matter.



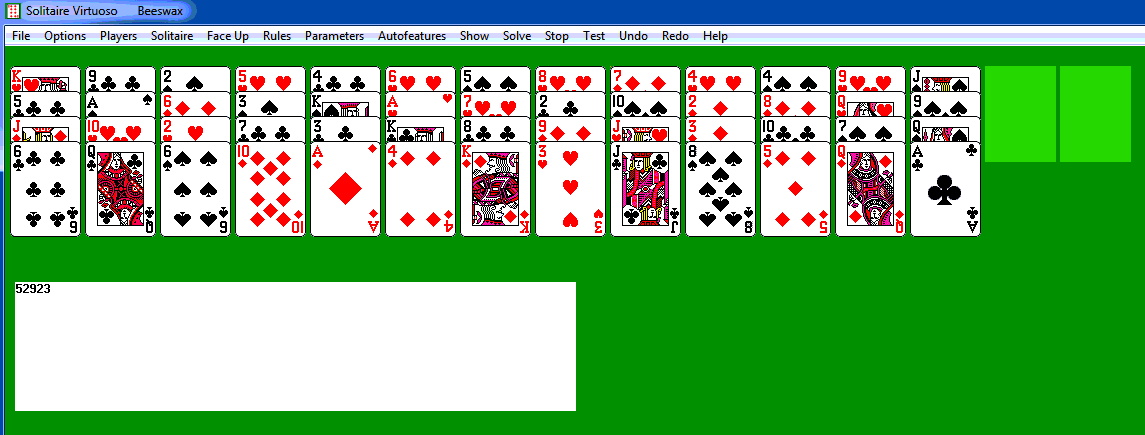
Let's play through a deal, number 52923, from Solitaire Virtuoso. Usually the player wants to move, if possible, three (or even on occasion four) cards of the same rank to one of the two empty columns, trying to keep one column empty as much as possible.  Often there are no ranks with three available cards, so we try to find a pair which will expose two more playable cards.  In this case moving the two aces to the first empty column will uncover a queen and a three, both of which can be played on.  The moves are notated, as in other column-packing games, using a hexadecimal extension of the standard FreeCell notation.  The columns are numbered 1-9 and A-F, and each move is specified by giving the starting and ending columns.  So moving the ace of diamonds to the first empty column is denoted 5E (this can be done quickly by right-clicking the AD, as in many Virtuoso games).  Moving the ace of clubs onto the ace of diamonds is DE.  We now have three queens free, and we can see that the fourth is in column C; if we can find places to put the seven of spades and nine of diamonds, we can get the four queens together.   We move all three queens into the last empty column, put the ten of diamonds on the ten of hearts, and complete a quartet by putting the queen of hearts on the other three queens.  Note the automatic recording of the solution.



Now we could regain a space by putting the nine of hearts on the nine of spades, but we can also clear column 2 if we can find a place for the two tens.  We can put them in column 9 if we can move the two jacks, so we put the nine of spades onto the nine of hearts, move the two jacks onto the jack of spades, the two tens onto the ten of spades, and the ace of spades and nine of clubs onto their respective columns.  Now we have an empty column again, and four clean columns (columns with cards all of the same rank).  We can also move the three of hearts onto the three of clubs and complete the quartet of nines with the nine of diamonds.  Sequences of plays like this are not hard to visualize with practice.



We can now clear column 3 by putting the sixes in column 2 and the twos in column 8; look for opportunities to clear columns with only two ranks in them whenever possible.   We also move the six of clubs and jack of diamonds onto their corresponding columns.  You should always move free cards into clean columns (columns containing only one rank) whenever possible, unless you have no empty columns and can create one by moving all of the cards from a clean column onto another column.  We also move the five of diamonds onto the five of clubs, uncovering the ten of clubs and setting up another set of maneuvers.  If we move all four tens into the empty column 3, and the eight of spades into the eight of diamonds, we can clear column 4 by putting the two sevens onto the seven of diamonds, the three of spades on the three of diamonds, and the five of hearts on the five of diamonds.  But instead of moving the five of hearts, we put the two fives from column 1 onto it, and we can instead clear column 7 by moving each of the four cards onto a different column (I call this a fountain, and try to finish a deal with a fountain when I can).  We're almost finished now:



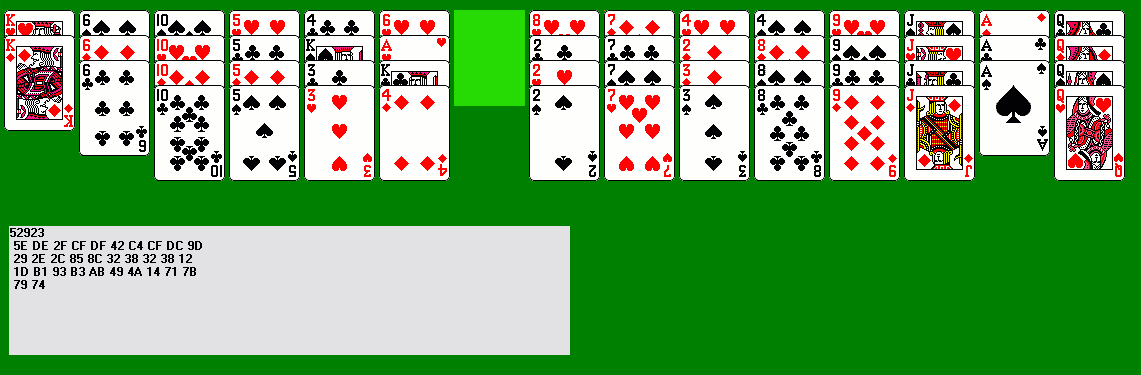
If we move all four threes (from columns 5 and A) into the empty column 7, we can clear column 6 (king of spades to column 1, four of diamonds to column 5; finish three quartets with king of clubs, ace of hearts, and six of hearts).  The last three quartets are easy -- all four twos to an empty column, then finish the eights and fours).  Our completed solution is:

52923
 5E DE 2F CF DF 42 C4 CF DC 9D
 29 2E 2C 85 8C 32 38 32 38 12
 1D B1 93 B3 AB 49 4A 14 71 7B
 79 74 57 A7 51 65 61 6E 62 86
 A6 B8 A5 B5

Like many open solitaires, Beeswax has a very high win rate with expert play (the standard game is over 99% by Mark Masten's analysis).   I have been able to win up to 98% of various blocks of 100 Solitaire Virtuoso deals given enough attempts, though I only win about 1 in 3 on the first try (without undos).  There is plenty of skill involved: I would rate this as one of the best open solitaires.    The game can also be played with varying numbers of ranks or suits: Solitaire Virtuoso supports up to eight suits.   Mark's analysis covers many variations, including versions with only one extra column (extremely unlikely to be winnable unless the number of suits is reduced to two, or the number of ranks are reduced) or three (probably almost always winnable even with five or six suits).   The larger version are extremely challenging: I have had only limited success with 5x13 and 8x8 games.

There is also a puzzle version which does not use cards, but colored balls or other objects (hoops, sand, water).  It goes by many various names, including Color Sort, Water Sort, etc.   Herbert Kociemba has several very detailed pages on this puzzle, including a downloadable solver able to find optimal solutions to puzzles with various parameters.  He includes source code and description of the algorithm.  I do not even know if the puzzle version was derived from the card game or vice versa.   I decided to give the game a new name because it is something of an open version of the second game we are looking at...

  

Beehive is a storehouse game rarely seen in books; my only sources are books on card games for children, Joseph Leeming's Games and Fun With Playing Cards (1980 Dover abridgement of an 1949 original), Alfred Sheinwold's 101 Best Family Card Games (Sterling, 1992), and Vernon Quinn's 50 Card Games for children (USPCC 1946, where it appears as Honeybee).  It is also rare as a computer game: until recently, I had only seen one version, no longer available, by NZP Games (their website no longer exists, but my 2005 copy of the game still runs in Windows 11!).   10 cards are initially dealt to a storehouse (only the last card is face up; others are turned face up as they are uncovered).   Six more cards are dealt, one each to six piles, to start the tableau; the remaining 36 cards form a stock.  The stock is dealt, three at a time as in Demon or Klondike, to a wastepile (NZP and Leeming both specify that the stock be dealt with only one card at a time visible, but I find games using the Demon deal much more strategic if you spread each group of three, as you will see in the sample deal).  If the top of the waste matches any of the tableau columns in rank, it may be moved there, uncovering another waste card.  When the stock is exhausted (possibly after dealing one or two leftover cards as a group), the waste can be turned over (without shuffling) and redealt, as many times as necessary.  When the fourth card of the same rank is moved to a tableau column, the quartet of four cards are discarded, and the empty column can be filled at any time with a card from the storehouse or waste.  Leeming specifies that an empty column must be immediately filled from the storehouse, or from the top of the waste after the storehouse is empty.  But the game is also much more strategic if a column may be left empty (NZP and Solitaire Virtuoso both allow this).  The object is to form and discard all 13 quartets of the same rank.   NZP uses a storehouse of 16 cards, but the game is probably too hard that way.  There is now a good version in BVS Solitaire, with the same 10-card storehouse specified in Leeming.  Solitaire Virtuoso uses a 13-card storehouse as a default; this can be changed to any value between 7 and 16.    Beehive is a good game for practicing strategic manipulation of the stock, which may help in other games (such as Demon or the three-at-a-time version of Klondike: Robert Abbott's site has a discussion of how to use this strategy in playing Klondike).

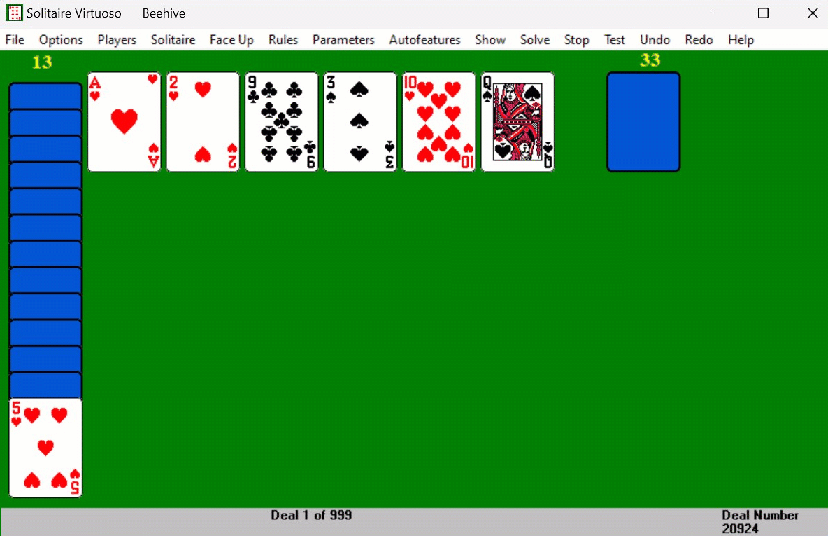
Above is a sample deal which we will play through, to illustrate some of the tactics in Beehive.   The initial deal of 20924 is shown above, with a storehouse of 13 cards showing the five of hearts, and six different ranks in the tableau piles: deals which provide no initial spaces are much more difficult to win, but this one works out.  Run through the stock once, noting which available cards in each turn of three can be matched to a tableau pile.  You should also note how many of stock cards match the rank of the current storehouse card: in this case all of the other fives are in the stock.  In this case, the sequence of available cards in the stock is 8,4,A,8,7,5,9,2,9,T,4; the matchable cards are boldfaced (we will refer to these cards as earmarked).  Generally we want to play these in reverse order: ten, nine, two (a pair of twos is available, which is underlined), nine, and ace.    We have also noted that one of the top cards is a five, the available storehouse card; this is also a pair.   The last five is also in the stock, but not available yet.  Recycle the stock by clicking on the empty space under the zero which shows the number of cards left.  Now turn through the stock until the ten of clubs appears in the next-to-last turn of three, and play both the ten of clubs and the queen of hearts which is available next.   Recycle the stock and turn again until the second nine (of hearts) appears, and play it.  The next turn of three shows the ace of diamonds; we are past the cards we earmarked on the first pass, so play the ace now.  That allows the two of spades to be played also.   Nothing else can be played on this pass, but when we recycle we will eventually reach a pair of twos which can be played, completing the twos pile, which is discarded automatically.   We can then play the nine of spades, which reveals the nine of diamonds and completes the nine pile also.   This reveals the three of clubs, which can also be played.  We are in good shape, with two empty spaces, two quartets complete, and an ace still earmarked in the third turn of three.  There are three fives in the stock, so we will play the five of hearts from the storehouse to one of our open spaces, and work to release the other fives (second diagram above).   This should be easy, as two of them are on top of a turn of three, and we have an empty space to help release the last.   In fact, when we turn the next three cards, the five of clubs appears; we know that the other two fives are available, so we play the five of clubs.    We know that we will be able to finish the five pile, so we play the two kings now available to the empty space, along with the king of clubs now available in the storehouse.   We turn to the end of the stock, noting that the last two cards are both fours.  We recycle the stock again; we have an ace and the two fives earmarked.   The first turn of three shows a king second; after we complete the five pile we can free that king by playing the eight into the space (this is a common tactic, freeing the second card in a turn of three to complete a quartet, and regaining the space).   Turn the stock until you reach the two fives, and complete the five pile, followed by the queen of clubs.   Recycle the stock and play the eight of diamonds and king of spades as we just mentioned, then the ten of spades which is revealed (playing all three cards from a turn will not disrupt the pattern of future turns).   The next three cards are not playable, but there is a four on top, and the last two cards are fours, so we can be sure of completing a quartet of fours if the other four is in the stock also.  The next three cards (ace of clubs, eight of spades, and queen of diamonds) can all be played, completing the queen pile, and the three after that shows the eight of clubs which can also be played.   At this point we have two spaces, and ten cards left in the stock.   It turns out that playing from the storehouse now will win easily, but we cannot see that, so instead we will start a pile of fours and extract the last three at the same time.   Recycle the stock and play the four of spades from the first turn,and the last two fours from the end of the stock.  Recycle again and play the three of diamonds.  Everything left in the stock is sixes and sevens, so we must play the jack of hearts from the storehouse, hoping to reveal one of the five cards we need to finish a pile.   It turns out that there are two more jacks, followed by a ten to finish the tens pile.   The seven of hearts is now showing in the storehouse, with six cards under it, five of which would finish a pile.    Unless the last six is directly below the seven in the storehouse, we will win easily, but what if it is the six?   The last six cards in the stock in order are 6,6,7,7,6,7.   It turns out we can play all four sevens anyway: play the seven of diamonds from the first turn of three (the second seven will become the top card of the first turn of three when we recycle), turn the last three and play the seven of clubs, recycle the stock and turn three to reveal the seven of spades, and play it.  Now the game is impossible to lose, as playing the seven of hearts from the storehouse completes seven quartets, guaranteeing that every card left can be played to one of the six available tableau piles.  (Anticlimactically, the next card in the storehouse is the three of hearts, so our clever maneuver didn't turn out to be necessary, but it might come in handy at some time.  In fact the fourth six was the last card in the storehouse).
  
Jan Wolter, for his online Polymorphic Solitaire package, devised a new interface for unlimited stock deals which he calls Gallery Mode; the whole stock is simply spread out in order, and allows any card to be selected in any order when the stock is dealt one a a time (as in the standard version of Klondike).  When the stock is dealt three at a time, Gallery Mode shows playable cards by jogging them upward.  This works well for Beehive, eliminating the need to cycle repeatedly through the stock, and making it less of a memory game.

{Sequence of deal 20924: 6D AS JC 4H 8H 3H 7H TD JD JS JH KC 5H AH 2H 9C 3S TH QS TS KS 8D 6C 6H 4C QD 8S AC 3D 7D 8C 7S 6S 7C QC 5S 5D 4D 3C 9D 9S 2C 2D KD KH 9H 5C QH TC 2S AD 4S}

Copyright ©2024 by Michael Keller. All rights reserved.  This file was revised on May 31, 2024.