Pyramid and Giza

Pyramid and Giza
by Michael Keller and Mark Masten

One of the more popular forms of card solitaire is Pyramid, in which 28 cards are dealt from a single deck in the form of a triangle of overlapping rows (below). In the most common form of the game, the remainder of the stock is then dealt one card at a time, and available cards are discarded in pairs adding to 13 (kings are discarded alone; any available queen (12) may be discarded with any available ace, jack (11) with two, ten with three, etc.). Stock cards which are not discarded when turned up are placed on the top of a waste pile. Cards available for discarding are any uncovered cards in the pyramid, the top of the waste, and the stock card most recently dealt. Discarded cards simply vanish from the game and play no further part. In the original version of the game, the stock is dealt once (there is no redeal). The object is to discard all 52 cards.

Par Pyramid

The beginning of a Pyramid deal: The king of clubs can be removed by itself; the jack of hearts and two of clubs can be removed as a pair (these two discards uncover the ace of diamonds, which can then be discarded with the queen of clubs. The three of clubs is not yet playable and starts a wastepile; the next stock card is the eight of hearts, which can be discarded with the five of spades. In the standard rules, the ten of hearts cannot be removed along with the three of diamonds which covers it, but we'll examine this rule later under Overlap Discards.

The traditional game is very difficult to win: Albert Morehead and Geoffrey Mott-Smith estimated the win rate at 1 in 50 to discard all 52 cards in one pass of the stock, though this is guesswork and the actual win rate with expert play may be even lower. They devised a variant called Par Pyramid in which the waste may be turned over to form a new stock (without shuffling) and redealt twice more, with a scoring system giving points for clearing all the cards of the pyramid (50 for the first pass, 35 for the second pass, 20 for the third), and a penalty of 1 point for each card left in the waste after three deals. This is one of the best forms of the game: I've played thousands of deals by computer and managed only a handful of perfect wins, clearing all 52 cards on the first pass. The scoring system, however, allows me to come out ahead in the long run.

There are a number of other variants of the game: many computer implementations only require the 28 cards of the pyramid to be deleted. It bothers me a little that many of these are presented as if they were the standard rules of Pyramid, rather than a variation. Several variants allow the stock to be dealt into multiple waste piles (using a Spider deal), or add a reserve of seven cards below the main pyramid. Trevor Day's 1996 Collins Gem Patience Card Games includes a version with two wastepiles: each unplayable stock card can be placed in either waste, which adds a strategy element similar to planners like Calculation, but oddly enough he doesn't seem to permit the tops of both wastes to be paired together. There is also one redeal of the combined wastes allowed. Adolfo M. Alonso's 2003 book Solitarios Con Cartas de Poker includes a variant with two 21-card pyramids, with a stock of ten cards which can be redealt once. All of these modifications are intended to make the game easier to win by making more cards available more quickly.

A Brief History of Pyramid

Originally an entirely different game went by the name The Pyramid: a forerunner of Carpet with a carpet of 15 cards dealt in a triangular arrangement without overlapping. This can be found as late as 1964, in Walter B. Gibson's How To Win At Solitaire. The modern game of Pyramid is almost certainly an American invention: it started appearing in various books under different names, while including the older game under its original title. Dean Bryden's 1927 Fun With Cards might be the first appearance of the modern version of Pyramid, under the title Elizabeth's Solitaire; he requires only the pyramid to be cleared, and gives a sample deal move by move. Johnson and Pope's 1928 book 30 Games of Solitaire may be the first book to include the modern Pyramid under its current name: they allow only one deal, but count it as a win to clear the pyramid, claiming a win rate of about 1 in 50. George A. Bonventure's 1930 Games of Solitaire includes it as The Tower of Twenty-Eight; he also allows only requires the pyramid to be cleared, but allows the waste to be redealt once. Helen L. Coops' 1939 book 100 Games of Solitaire also uses Tower of Twenty Eight (she drops the article from all her names, which is the modern practice), including it among games like Baroness. She allows no redeal of the waste, and requires all 52 cards to be discarded. Coops, like Bryden and Bonaventure, includes the older Pyramid; she also gives Pike's Peak as an alternate title, and lists The Carpet as a variant. [I suggest that Pike's Peak might be adopted as the standard name for the Carpet forerunner, as Pyramid now refers to the modern game we describe here. Pike's Peak was probably coined by Benjamin Newton, who borrowed games from Dick's Games of Patience for a book in the 1880's, renaming them all.] Pyramid appears under its modern name again in Games Digest in March 1938, where the author suggests it is next to impossible, and calls twelve cards left (counting both pyramid and waste) a successful result. After the publication of Morehead and Mott-Smith's The Complete Book of Solitaire and Patience Games in 1949 (which also saw the debut of Par Pyramid), Pyramid became well-established as a part of the standard repertoire of solitaire games, at least in the United States. Several sources cite Pile of Twenty-Eight as an alternate name, but I have not yet found a source which uses that as the primary name.

The structure of the pyramid and win rates

Blocked Pyramid

An impossible deal: it is not even necessary to start dealing the stock to see that the pyramid can never be cleared. The tens of diamonds and spades are covered by three of the threes, and there are only two tens left to remove them. The ten of hearts can eventually remove the three of hearts, but the ten of clubs in the stock cannot possibly remove both the remaining threes.

Mark Masten has designed a Pyramid solver and has run millions of deals to examine the win rates of some typical variants. The first variant used an open bouquet of 24 cards which are available simultaneously. This is essentially equivalent to dealing the stock with unlimited redeals, and was designed to determine what percentage of losses were due to the structure of the pyramid itself. Many arrangements of 28 cards are inherently blocked, sometimes due to the positions of one set of eight complementary cards (as the tens and threes in the diagram above), and sometimes due to more complex crossblocks involving several sets of ranks. Based on 100 million random deals, the pyramid is blocked almost one-third of the time: the solver won 66,865,010 deals out of 100 million. More than 10 percent of deals (10,659,494) were blocked due to a card being covered by all four cards of the complementary rank: a program which detected and removed such obviously blocked deals would boost the win rate to almost 75 percent with unlimited redeals. The appendix contains much more data, including variants with pyramids ranging from 5 to 9 rows.

Mark also analyzed the one-pass version, though the solver uses knowledge of the exact sequence of cards in the stock. This technique, called thoughtful play, is used by computer solvers to set an upper bound on win rates for closed games, like Klondike, which would be hard to analyze otherwise. It differs from the open bouquet version in requiring the stock cards to be played in order or discarded to the waste, though it is still possible to backtrack through the waste. Out of a sample of 1 million deals, the solver cleared the pyramid 82,735 times, and discarded all 52 cards 60,268 times. The percentage of wins is much higher than I anticipated, though it is likely a human player without knowing the order of the stock will not be able to get close to 6%, except by using undos or replaying the same deal.

Overlap discards

One variant which is frequently seen is to allow a card to be lifted, uncovering a complementary card beneath it, and then discarding both cards (the card underneath must be covered only by the card it is being discarded with). I refer to this as an overlap discard; it can also be used as an optional rule in other discarding games such as Fourteen Out or Nestor (where it would apply to rank pairs). In the previous example, after the four of spades is discarded, it is then permissable under overlap discards to remove the five and eight of clubs together. Overlap discards also greatly affect the percentage of blocked pyramids: in the example above, it would be possible to discard all of the tens: ten and three of hearts, ten of clubs (from the stock) and three of diamonds, ten and three of spades (overlap), and finally three of clubs (from the stock) and ten of diamonds. Mark's solver looked at the same 100 million deals, with an open bouquet of 24 cards, and found that allowing overlap discards cut the number of blocked deals almost in half: the solver won 83,151,588 deals when overlap discards are allowed. It's not clear which version is more strategic: making an overlap discard may not always be the correct play, so a player will have to use judgement in either case. (Solitaire Virtuoso allows overlap discards as an option). In the one-pass version, the solver looked at the same 1 million deals as above, clearing the pyramid 212,975 times, and discarding all 52 cards 143,310 times (about 1 in 7).

Tutenkhamen's Curse, or Pyramid Puzzlements
(Why Pyramid Must Have The Top of The Stock Available)

In 1990, Microsoft released the second of its Windows Entertainment Packs, which contained two card solitaires. The first of these was FreeCell, which became a worldwide phenomenon. The second was a variant of Pyramid called Tut's Tomb, which did not. Tut's Tomb features (in one variant) a three-at-a-time deal from the stock to a wastepile (lifted from the game Demon). [The alternate version, where the stock is dealt one card at a time without a redeal, is pretty well hopeless.]. The top of the stock is not available, and the top of the waste can only be matched with an uncovered card from the pyramid. The object of the game is to clear the pyramid of 28 cards only, and while the game is playable (i.e. it can be won occasionally), it is much less interesting than most Pyramid variants where all 52 cards must be discarded -- the skill in playing Pyramid lies in knowing what matches to make and which to pass up, and when to match stock-to-waste and when to match within the pyramid. Tut's Tomb allows overlap discards: a card in the pyramid can be matched with a card directly underneath it if that card is not covered by any other card. This helps somewhat, as we have seen earlier.

In some versions of the game, the object is to discard all 52 cards. What does this mean? Since every card from the stock of 24 (except kings) must be matched with a card from the pyramid of 28, it means that if all four kings are on the pyramid, there can be no pyramid-to-pyramid matches. Each king in the stock leaves room for one pyramid-to-pyramid match. Since most pyramids require a few matches within the pyramid to unblock troublesome ranks, this makes breaking down the pyramid extremely difficult. [Some computer versions of Pyramid make a different mistake, automatically discarding both cards (if they are complementary) when the top of the stock is placed on the waste to make room for a new stock card. Frequently one needs such a pair to break up a pair in the pyramid, especially where one is covering the other. See below for some solver data on how much of a difference this makes.]

But the situation is worse than that. Since stock-to-waste matches are not possible, the stock cannot contain more than four of any pair of complementary ranks (e.g. if there are 2 fives and 3 eights in the stock, there will be no way to discard the last one of each). Some of the pairs may have less than four, the combined shortfall being the same as the number of kings in the stock. What are the odds of the stock containing a suitable combination of ranks? I did a combinatorial calculation (some mathematically inclined reader may care to confirm this) showing that 5.547 percent of the deals are acceptable -- a computer simulation of two million deals also gave a figure slightly above 5.5 percent. This means that if you cannot pair up within the stock, you can win at Pyramid 5-1/2 percent of the time if any card from the stock can be matched with any complementary card from the pyramid regardless of its location. Since the pyramid's shape makes cards available only gradually (and we now know that about a third of pyramids are inherently blocked), and the three-at-a-time deal makes matters worse, I can't imagine the win rate being more than about half a percent, and perhaps much less. And that win rate assumes that the player knows that the number of pyramid-to-pyramid matches is limited by the number of kings in the stock.

Pyrimpos.gif (15764 bytes)

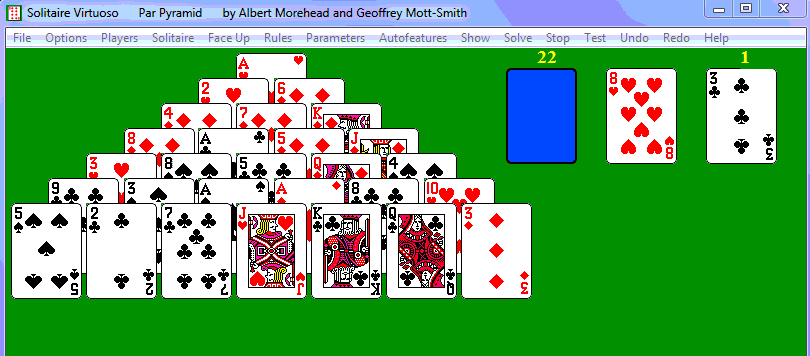
An impossible deal: If the top of the stock is not available to be matched with the top of the waste, this Pyramid deal (screen shot from the Solitaire Laboratory program) cannot be won. There are two queens and three aces in the stock, and when three queen-ace matches have been made between the stock and pyramid, there will be one queen and one ace left in the stock and no way to discard them.

Pyrpos.gif (14805 bytes)

A possible deal: There is one king in the stock, thus 23 non-kings in the stock and 25 in the pyramid. One pyramid-to-pyramid match will be possible, which must be a jack-two match, specifically the jack of hearts and two of diamonds (the only two which is neither covers nor is covered by the jack). Such deals occur infrequently, and most have three or four kings in the stock. All other matches must be stock-to-pyramid.

When King Tut (modeled after the original Tut's Tomb) first appeared in Pretty Good Solitaire in 2001, the rules specified that all 52 cards must be discarded, and yet the Top Scores page listed 42 wins out of 408 tries. I suspect that some people were submitting doctored stats (interestingly, neither of the players who at that time had played enough games to be listed individually had won even once.) BVS Solitaire Collection's top score pages do not appear to have the same game, so I cannot compare its stats. King Tut's rules were later modified to require only the pyramid to be cleared. I still don't consider it to be a good game (much better is the three-deal Par Pyramid, with one card at a time dealt and the top of the stock available); I consider the three-at-a-time deal to be an overused mechanism which doesn't work well in most games, including Pyramid.

Does anyone out there have a fully winnable deal of King Tut (i.e. a deal number which can definitely be won by discarding all 52 cards)? I'm curious to know if there is anything wrong with my analysis.

The same mistake can be found in a number of other computer versions of Pyramid. Well-written books are explicit in allowing the top of the waste to be matched with the next card dealt from the stock.

(Tutenkhamen's Curse was originally published as an independent article in 2004.   The data below was added in 2021.)

The Pyramid solver has results when stock-to-waste discards are not allowed, with the stock dealt once, based on a million deals. In the best scenario, with overlap discards allowed and the object only to clear the 28 cards of the pyramid, the solver won 115,484 games (11-1/2%). Without overlap discards, the pyramid was only cleared 34,242 times. It wasn't immediately obvious to me why clearing the pyramid is so much harder without being able to make stock-waste discards.   The answer is that many deals require backtracking through the waste pile just to clear the pyramid, and this is frequently impossible when the waste is clogged with adjacent pairs which could not be discarded because of a faulty rule.

When the object is to discard all 52 cards, the results are much worse. Even with overlap discards, the solver only won 1119 times (a little better than 1 in 900 games); without them, it managed only 678 wins (slightly above 1 in 1500).

The solver also has results when the stock and top of waste are automatically discarded when they match.   For the same million deals, the solver cleared the pyramid 186,390 times with overlap discards and only 65,234 times without.   All 52 cards were discarded 128,051 times with overlap discards and only 48,087 times without.   It is definitely still a mistake for a program to make automatic discards (usually because one of the pair is needed to remove a pyramid card), but nowhere near as disastrous as making them impossible. (But remember that the solver knows where all of the stock cards are, and may avoid some of the times when a stock-waste match would be wrong by matching one of them with a pyramid card at the right moment).

The Pyramid Solver in Action

Solver example

Here is an example deal generated by Mark's solving program. Under standard rules, without overlap discards, the program was able to win by discarding all 52 cards. With either automatic stock-waste discards, or no stock-waste discards, the program was unable to even clear the pyramid. You have all the information the solver has: all 24 stock cards are shown in the order they were dealt, left to right.   Can you find the win? As a hint, the solver finished the game with a long series of mostly waste-pyramid discards, after the last stock card was dealt.   The full solution is given in the Appendix.

Summary of solver win rates for various rules (Thoughtful Pyramid)

                  Overlap Discard? Open One-Pass No Stock-Waste    Automatic                 6x4
                                                        Matches      Stock Matches     Giza     Giza
Discard Pyramid         Yes                21.30     11.55           18.64
                         No                   8.27        3.42            6.52
Discard All Cards       Yes         83.15    14.33        0.11           12.81        59.29     38.49
                         No         66.87     6.03        0.07        4.81        36.53     18.05

Giza -- a solitaire based on Pyramid -- by Michael Keller

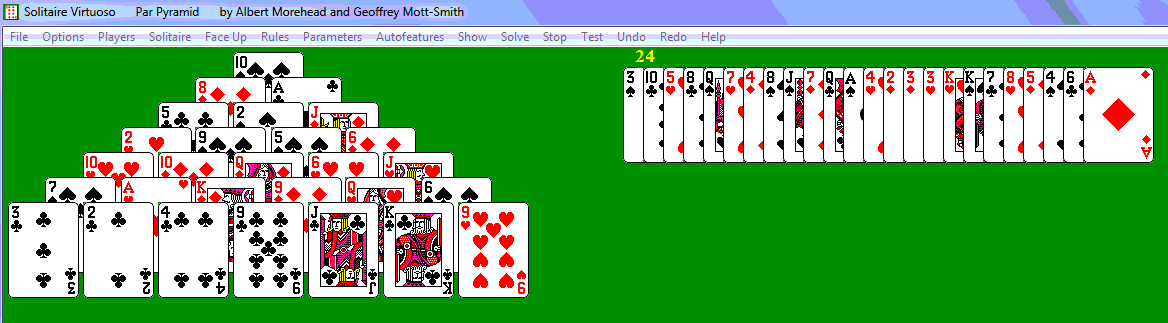
With all of the Pyramid variants in mind, I had the idea around 1996 to turn Pyramid into a completely open solitaire (one in which all of the cards are dealt face up at the start of the game) like FreeCell; such games are usually very skillful and puzzle-like. I tried a number of different tableaux; my original idea was four rows of six columns each below the pyramid, but this blocked too frequently. I also originally tried an upside-down pyramid, but the need to uncover the first few cards dominates the game and the latter part of the game is anticlimactic. Experimentation proved that three rows of eight cards (as in the picture below) worked best. I called the game Giza, after the location of the great Egyptian pyramid. Several hundred games suggested that the win rate is at least 1 in 3 with careful play, although many of the wins are very difficult and 1 in 4 is a reasonable goal. I wrote a computer version in 1997, and the game was first published in 1998. Other computer versions of the game for Windows can be found in Boris Sandberg's package BVS Solitaire Collection, Thomas Warfield's Pretty Good Solitaire, and Michael McCulloch's Solitaire Plus.

Mark Masten has analyzed Giza with his solver, dealing 10 million deals. The solver won 3,653,287 deals under the standard rules (so the win rate is above 36%), and 5,928,825 with overlap discards permitted in both the pyramid and tableau columns. You are of course free to play whichever version you prefer. You can even try the much harder six-column game: the solver won 180,527 out of a million deals with standard rules, and 384,911 with overlap discards.

Here are some difficult Giza problems I have found to date; the first is number 2112 in Solitaire Virtuoso. Any uncovered king, or any two uncovered cards adding to 13, may be removed (e.g. the four of diamonds may be removed along with either the nine of diamonds or the nine of hearts). No overlap discards are allowed in these problems: a card may not be removed along with a card it is covering (the queen of clubs cannot be removed along with the ace of diamonds). Can you discard all 52 cards?

giza2112.gif (20656 bytes)

Here is number 15849 (solution):

giza15849.gif (21057 bytes)

And here is number 50832 (solution):

giza50832.gif (20415 bytes)

Appendix

Blocked pyramids of different sizes

Rows Overlap     Wins   Simple    Adjusted    Bouquet
      Discard?             Blocks    Win Rate

5      Yes     99639563    206435     99.85        37
         No     98625648 459637     99.08

6      Yes     96923906 1501149     98.40        31
         No     91893246 2592145     94.34

7      Yes     83151588 7167001     89.57        24
         No     66865010 10659494     74.84

8      Yes     38349300 25275626     51.32        16
         No     16303005 33593656     24.55

9      Yes      1279299 63905021     3.54         7
         No      71531 75562119     0.29

This table gives the number of wins, out of a sample of 100 million deals, with each size of pyramid from 5 to 9 rows, with and without overlap discards. Any cards remaining after the pyramid is dealt form an open bouquet (from 37 cards in the 5-pyramid to just 7 in the 9-pyramid). Also listed are the number of deals in which a card is blocked by all four of its complementary rank, and the adjusted win rate if these deals are excluded by a computer program (or by visual inspection by a player, who may then choose to skip the deal without playing a card).

Solution to the solver example

The solver starts by discarding the KC and the 9H/4C (the solver wanted to expose 6S early, though discarding 9C/4C would work as well). After dealing the first two stock cards, it takes the pyramid 3C off with the TC. Already the automatic stock-waste discard would have lost: the 3S is going to take off the TS at the finish. You can actually start to see some of the program's logic: it plans to set up a set of discards at the finish with the first several waste cards and the last several pyramid cards, working backwards through the waste. The next three stock cards don't play with available cards, but match up perfectly with the pyramid (5H/8D, 8C/5C, QS/AC), so the solver does not discard 5H/8C. Now the 7H is dealt and takes the 6S with it (the solver's reason for discarding the 9H instead of the 9C, although it doesn't matter in the end since a four comes next in the stock). The 4D takes off the 9C, freeing the KD to be discarded alone. The 8S doesn't play, but is earmarked for the 5S. At this point, it passes up some possible pyramid plays, instead discarding the JS/2C, and dealing five more stock cards, finally removing the 2D/JC. This seems counterintuitive, but the program knows the order of the stock cards and wants to match them in the correct order with the pyramid. Now it takes off QH/AH and 4H/9D. AS/QC is no longer legal, since both were already in the waste. Instead it takes off AS/QD and 7S/6H. The two threes coming next in the stock take off the two tens on the pyramid in either order, then JH/2H, followed by the two stock kings.

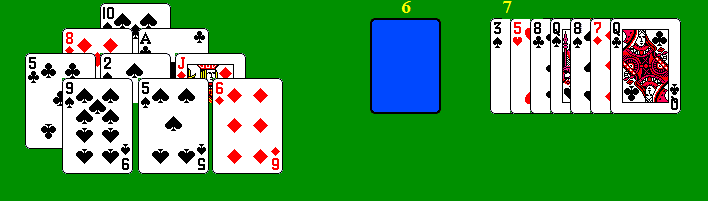
Solution finish

At this point there are six cards left in the stock and nine on the pyramid, and the solver can visualize the finish. The 4S will take off the 9S, and there will be three stock-waste discards (the only three in the entire solution), leaving the rest of the waste (in reverse order) to take off the pyramid cards (with one pyramid-pyramid discard interpolated). 7C is skipped (6D is earmarked for 7D), then the next two cards (8H/5D) are discarded -- this is the first stock-waste discard the solver has made. Now the 4S takes off the 9S, and the 6C/7C becomes the second stock-waste match. The last stock card, the AD, takes off the QC in the waste, and the rest follows easily: 7D/6D, 8S/5S, 2S/JD (both in the pyramid), QS/AC, 8C/5C, 5H/8D, and 3S/TS. [When the solver was given the same deal with overlap discards allowed, it played the same solution, except that it made the early 5H/8C stock-waste match and took 5C/8D as an overlap discard.]