FreeCell -- Frequently Asked Questions (FAQ)
written by Michael Keller, Solitaire Laboratory

This article is the result of more than 20 years of work by me and a small group of like-minded FreeCell enthusiasts. You may freely link to it from your website, but please do not plagiarize its contents.

Thanks for questions and answers to:
Kate Ackley, Brian Barnhorst, David Bernazzani, Marion W. Berryman, Bill Borland, Yuri Bortnik, Frank Bunton, Wilson Callan, Gary Campbell, Vickie Caster, Mike Cochran, Dennis Cronin, Jason A. Crupper, Cheryl Davis, Jason Dyer, Mike Dykstra, George W. Edman, Vince Egry, Adrian Ettlinger, Karl Ewald, Shlomi Fish, Andy Gefen, Dan Glimne, Kenneth Goldman, Micah Gorrell, John Hironimus, Tom Holroyd, Jim Horne, Brian Jaffe, Danny A. Jones, Scott Kladke, Dave Leonard, Brenda Marriott, Martin E. Martin, Mark Masten, Joe McCauley, Rick Mendosa, David A. Miller, Ryan L. Miller, Mike Moak, Charlotte Morrison, Jonah Neff, Jo Ann Perry, Madeleine Portwood, Ingemar Ragnemalm, Bill Raymond, P.L. Richart, Dave Ring, John Ross, Ronald P. Ross, Richard Schiveley, Greg Schmidt, Frankie Seidel, Laurie Shapiro, Lowell Stewart, Judy Stratton, Terry Thomas, Thomas Warfield, Brent Welling, George West, Don Woods, and Clinton Yelvington.

Please report any errors (even typos), broken links, omissions, or suggestions for additional questions to me.

A catalog of selected solutions to the standard FreeCell deals, begun by Dave Ring and later maintained by Wilson Callan, is now located on this site.  It is now a single file.  It is retained for historical purposes, as it contains a number of specialized solutions, including zero-freecell and flourish solutions.  There is at least one complete catalog available elsewhere for the extended set of 1 million deals.

Table of Contents
1. General Information
* Who invented FreeCell? How did it get started?
* Why is FreeCell so popular?
* What has been written (off-line) about FreeCell?
* What are the rules of FreeCell?
* How does autoplay work?
2. The Microsoft 32,000
* Can they all be solved?
* Why doesn't Microsoft FreeCell always tell me when I have lost?
* Which deal is the hardest to solve?
* How are the deals numbered? Are those deals random or were they selected in some way?
* Does the program automatically turn up deals which have not been won?
* How can I get the solution to a hard deal I can't solve?
* Why am I finding deal number xxxxx difficult when it isn't on any of the lists?
* Has anyone found a solution for Freecell xxxxx? It seems awfully difficult because of the remote positions of the aces.
* I have a streak of xxxx wins in a row and have won xx% of the deals I have played. How does that compare to other players?
* Are all of the solutions in the catalog correct?
* Why won't you post every new solution submitted?
* Why won't you post improved (shorter) solutions in the catalog?
* Which deal is the easiest? Are there any deals in which all of the cards go automatically home at the start?
3. Variations and Related Games
* I'm getting awfully good at FreeCell. How can I make the game more challenging?
* Can I play with a different number of columns?
* What is Ephemeral FreeCell?
* Is it possible to win without using the freecells?
* Why is it required to use freecells or empty columns to move sequences?
* Is it possible to get all 52 cards to the homecells at once?
* Can a card be played once it has been placed on a homecell?
* What are some other solitaires closely related to FreeCell?
4. Computer Versions and Features
* Is it cheating to use computers?
* What are the minimum requirements for a good computer version of FreeCell?
* What is FreeCell Pro? What can it do that most other programs cannot?
* What are some other programs which allow you to play FreeCell?
* Are there versions of FreeCell for Macintosh or other systems?
* Are there any handheld versions of FreeCell?
* What other computerized solvers exist?
5. More Statistical Facts and Curiosities
* How often can I win?
* How many freecells are needed to solve any possible deal?
* What is a supermove? How does it help in playing?
* How many possible FreeCell deals are there?
* What is the fewest number of cards one can have left remaining and still lose?
* Is it possible to play an entire suit to the homecells ahead of all of the other suits?

1. General Information

* Who invented FreeCell? How did it get started?

The idea of a game with temporary storage locations to hold single cards is not new. One of the oldest games of this type is Eight Off, which provides eight freecells (called depots in some older books) which can each hold one card at a time. The tableau consists of eight columns of six cards each, with the four remaining cards being dealt initially to four of the eight freecells. Cards may be packed (built on the tableau columns during play) downward in suit, not in alternate colors as in FreeCell. The foundations (homecells in FreeCell terminology) are built up in suit just as in FreeCell, but empty columns can be filled only with kings. In Martin Gardner's June 1968 Mathematical Games column in Scientific American (reprinted in his 1977 book Mathematical Magic Show), he describes a game by C.L. Baker which is a variant of Eight Off. Baker's Game, as it is now called, differs from Eight Off in having only four freecells instead of eight -- the four extra cards are dealt to the first four columns. An empty column may be filled with any card, not just a king -- this allows them to be used as temporary storage areas too, and allows large sequences of cards to be moved from one column to another. This makes a better, more interesting game in my view, though it is harder because it has only four freecells instead of eight. (An excellent online version of Baker's Game is available under the trademark Brain Jam; their home page also has a link to an old Windows version.)  An important feature of most of the games of this family is that unlike Klondike, only one card at a time can be moved, although computer versions allow a sequence of cards to be moved as a unit if they could be moved one by one using empty freecells (and/or columns).

Paul Alfille had the brilliant idea of changing Baker's Game in one respect, allowing cards to be packed on the tableau downward in alternate colors, as in familiar games like Klondike and Demon (Canfield), thus producing the game we know as FreeCell. This has the happy effect of making nearly every deal winnable, though many are still quite difficult. Alfille wrote the first version of FreeCell for the PLATO educational computer system in 1978. The popularization of the game is also due to Jim Horne, who wrote a character-based version for DOS and later a full graphical version for Windows. The latter first appeared in 1992 on Microsoft Entertainment Pack 2 (and later in the Best of Microsoft Entertainment Packs). Later versions were bundled with Windows For Workgroups and Win32s (the 32-bit extension to Windows 3), and eventually with Windows 95 (and 98). Dennis Cronin also wrote a freeware version for UNIX in the mid-80's, and undoubtedly there were other character-based versions floating around too. Both Horne and Cronin learned the game from the PLATO system. Thanks to the people at Cyber1, a version of PLATO is available online (thanks to Mike Cochran for help), and I have been able to try out Alfille's original Free Cell (as it was spelled there). It does not have numbered deals (though users can save interesting deals and share them with the PLATO/Cyber1 community), but has options for 4-10 columns and 1-10 freecells, with a statistics page showing the overall win rates of the community of players. You need to register to get access, but registration is free.

Two correspondents in Sweden, Dan Glimne and Ingemar Ragnemalm, uncovered a closer predecessor to FreeCell, which dates back at least to 1945. In his book Världens bästa patienser och patiensspel (The World's Best Patiences and Patience Games) Einar Werner (European bridge champion in his day) describes a solitaire called Napoleon på S:t Helena (Napoleon in St. Helena), which bears an extremely close resemblance to FreeCell. The differences are that the last four cards of the stock are dealt to the four freecells rather than the first four columns, and only kings may be placed in empty columns (called KingOnly by Thomas Warfield). These two differences make the game much harder than FreeCell, but it can be definitely stated that a relative of Eight Off with alternate-color packing existed more than 75 years ago. Thomas Warfield has suggested calling the game ForeCell, since it is a forerunner of FreeCell, and he has implemented ForeCell in the edition of Pretty Good Solitaire released in March 1999. One of the books which describes ForeCell is Lägga patiens by Svend Carstensen, a 1971 translation of a Danish book. The book estimates the chance of success for ForeCell at 1 in 10, which is well short of the mark. I played a block of 100 consecutive ForeCell deals using Pretty Good Solitaire, and I was able to win 36 out of 100 on the first try, and a total of 71 deals including multiple tries. Some of the deals can be clearly seen to be hopeless, but I estimated that the overall win rate for ForeCell with perfect play was probably in the range of 65-75 percent. This also turned out to be rather low; Danny A. Jones later analyzed the game using his solver, and found that 27,395 of the 32,000 MS deals could be solved using the rules of ForeCell. This suggests a win rate over 85 percent. In 195 of the deals (much less than 1 percent) no moves at all are possible. Of the 4605 impossible deals, 3897 are impossible even if the KingOnly rule is dropped; filling the freecells has a much larger effect than the KingOnly rule.   Solvitaire has also analyzed ForeCell, running 10 million deals with a win rate of 85.6%.

* Why is FreeCell so popular?

I believe it is primarily because of the puzzle-like nature of the game, and the fact that nearly every deal can be won. Most solitaires (including the most popular ones like Klondike, Spider, Pyramid, Forty Thieves, and Miss Milligan) can be won less than half of the time even with perfect play. Almost every FreeCell deal can be won if played correctly; it has one of the highest win rates of any solitaire (Accordion and Fortune's Favor, among others, are probably higher), yet individual deals run the gamut from trivially easy to excruciatingly hard. FreeCell is an open solitaire, meaning that all of the cards are dealt out face-up at the start, and the effect of any series of moves can be worked out, without having to rely on judgement and probability as in games like Klondike. FreeCell also differs from most of its relatives in using alternate-color packing on the tableau, a feature which has proved its popularity in Klondike, Demon (Canfield), and many other solitaires. Alternate-color packing gives the player a much wider range of plays than in-suit games like Baker's Game and Seahaven Towers, and also makes the win rate somewhat higher.

FreeCell led the voting in two online popularity polls for solitaire. In David Bernazzani's poll on his Solitude site, FreeCell won the voting with 824 out of over 4000 responses, well ahead of Klondike at 403, Pyramid at 269, Aces Up at 248, Spider at 176 (Microsoft added a version of this game to Windows ME/2000/XP), Golf at 159, and Canfield (i.e. Demon) at 128. In Thomas Warfield's poll at the Pretty Good Solitaire site, out of more than 850 votes, FreeCell won with 66 votes, ahead of Aces and Kings (one of Warfield's many inventions) at 47, Klondike at 41, Demons and Thieves (another Warfield original) at 33, Forty Thieves at 28, and Yukon at 24.

For some reason, FreeCell seems to have spawned an unusual number of urban legends (look up FreeCell on Yahoo! Answers, e.g.). We will try to dispel these legends here.

* What has been written (off-line) about FreeCell?

Despite its popularity in the online world, very little on FreeCell has appeared in print. I wrote an article for Games Magazine (Michael Keller, Big Deal, June 1995, pages 10-13) about FreeCell and Baker's Game. Dan Glimne's book of card games, in Swedish, published in December 1998 by Frida Forlag AB (Stockholm), 100 Kortspel & Trick: som roar hela familien (100 Card Games and Tricks to Entertain the Whole Family, ISBN 91-973473-0-2), was to my knowledge the first book of solitaires or card games to describe FreeCell (pages 66 and 67). The first English-language book of games to include FreeCell appeared in December 2001: the third edition of Hoyle's Rules of Games by Philip Morehead (384 pp., $6.99, ISBN 0451204840, Signet). Martin De Muro published solutions to the first 1000 MS deals in book form (Free Cell Game Solutions #1, January 2000, 338 pp., $19.95, ISBN 096763881X, self-published), available from on-line bookstores such as Barnes & Noble or Amazon. A new (2004) solitaire collection which includes FreeCell is 100 Best Solitaire Games by Sloane Lee and Gabriel Packard (188 pp., $9.95, ISBN 1-58042-115-6, Cardoza).

* What are the rules of FreeCell?

I guess it's easy to assume that everyone reading this FAQ or the mailing list knows how to play, but I have seen this question asked on newsgroups, and apparently not everyone finds the explanation in the Microsoft help file adequate. It is also not uncommon to see the rules wrong in computer versions (the most common mistake being to allow only kings to be placed in empty columns). I have also had questions from people who don't understand the rules well enough to know why they have (or haven't) lost. The rules are explained clearly, I hope, in the beginners' tutorial. One important point is that a sequence of cards can be moved only if it would be possible to transfer the whole sequence by moving one card at a time, using empty freecells and/or columns. This is very important in understanding supermoves as well as when playing with less than four freecells.

* How does autoplay work?

All good computer versions of FreeCell (of which there are now hundreds) have some facility for moving cards automatically to the foundations (homecells).  Some only do so when all of the cards are in sequence (autofinish), but most play cards to the foundations whenever it is safe to do so.   Aces can always safely be played, as well as twos of any suits whose aces are already there.    In general, it is completely safe to autoplay a card when any possible card that could be packed onto it on a tableau column has already been played to the foundation, or can be played there as soon as it is uncovered.    For example, a seven of diamonds is safe to autoplay (onto a six of diamonds already there) when both black fives and the four of hearts are already on the foundations.   The only cards which could still be packed on the seven of diamonds are the black sixes and the five of hearts (all of which could be autoplayed), since both black fours are gone.   This rule was implemented at least as early as Marc L. Allen's 1992 program, and is currently implemented in NetCELL, among others.   This rule applies even when worrying back (putting cards from the foundation back into play on tableau columns) is allowed.   It applies as well to Klondike and other similar games with packing in alternate colors.

Microsoft did not fully implement this rule, at least in its early versions of FreeCell: it does not autoplay the seven of diamonds in the above situation until both black sixes have been played to the foundation.  However, in that case it extends the rule and plays the seven of diamonds regardless of how many hearts have been played to the foundations, since nothing can now be packed on the seven of diamonds.  (If either black six was still in play, and only (e.g.) the ace of hearts was on the foundation, the seven of diamonds could conceivably be needed to pack a black six and the five of hearts).   If worrying back is allowed, the Microsoft extension is not safe: you might need to move the five of hearts (e.g. to empty a freecell or unblock a lower card) by worrying back a black six onto the seven of diamonds.

2. The Microsoft 32,000

* Can they all be solved?

All of the 32,000 Microsoft deals except for number 11982 are solvable.

Jim Horne's version for Windows 3.1 contained 32,000 numbered deals (games), so that selecting a specific number would always produce the same deal. (These are random deals, generated by integer seeds using the random number generator in the Microsoft C compiler). He numbered the deals so that people could exchange the numbers of difficult/interesting deals with their friends, and also in the belief that some people would try to play sequentially through the deals; many people have in fact done so. Happily, when the game was ported to Windows 95 and later operating systems, the set of 32,000 deals was the same, so any discussion of deal numbers applies to all Microsoft versions. The help file for Microsoft FreeCell contains the claim "It is believed (though not proven) that every game is winnable." When Horne wrote this, he already knew that unsolvable deals could be constructed (see Hans Bodlaender's example): as a joke, the Windows 95 version includes two unsolvable deals, numbered -1 and -2. Horne purposely made his claim ambiguous in order to challenge people to find such impossible deals, but intending it to mean that all of the 32,000 included deals were winnable. This comes as close as possible to being true...

Another factor in the popularity of the game, besides Microsoft providing the game free with Windows 95, was Dave Ring's Internet FreeCell Project. In August 1994, Ring solicited volunteers on rec.puzzles, sci.math, and elsewhere (eventually getting more than 100 people involved), and coordinated the volunteers in an effort to solve all 32,000 of the deals in the Microsoft versions. He assigned each volunteer a set of 100 consecutive deals, and the volunteers would report back after they had solved (or tried to solve) all 100, when they would be assigned another set if interested. Ring would reassign any deals reported as unsolved to his best solvers. I didn't get involved in the project until November 1994, but still managed to solve 1,970 deals. The project was completed in April 1995, and all but one deal was reported solved! This is the famous number 11982. I wrote the article on FreeCell and Baker's Game for Games while the project was still finishing up. Dave Ring wrote to Games shortly after the article appeared, reporting that the project was finished. Games printed Ring's letter, along with a layout of the unsolved number 11982, in the October 1995 issue (page 4). A report that 11982 had been solved turned out to be incorrect when it was discovered that the solver was playing Baker's Game (by hand) rather than FreeCell. I have since heard from almost two dozen players (Doug Schmieskors, Laura Ross, Martin E. Martin, Adrian Ettlinger, Freya Wieneke, John Williams, Dick Belmont, Don Rop, Morrie Hoevel, Ginger Martin, Bob Rankin, Wolfhart Wünsche, Rich Hook, Sheridan Wilson, Roberta C. Hendrickson, Emilien Fenez, Milli Stelling, Fred Lamon, Margaret Bannister, Theodore Gregg, Ken Gauvreau, Joyce DaFonte, and David B. Bowie) who have played the entire set of 32,000; most have won all but deal number 11982.  11982 has now eluded solution by probably thousands of human solvers, and at least eight independent computer programs I am aware of (most of which are designed to search exhaustively for a solution), and I am confident in calling it impossible:



A large catalog of solutions to (mostly difficult) deals, including all of those reported as hard during the Ring project, can be accessed from the main FreeCell page, along with other FreeCell information and links. The solution catalog was begun by Dave Ring, and was later maintained by Wilson Callan, and even later by me.  I am no longer doing so, since there are complete catalogs of solutions available now; the catalog is still available as a kind of historical record. You can look in the index to find out whether a particular solution is included. Probably the first large-scale computerized statistical study, conducted by Don Woods in 1994, analyzed a million random deals. In 1995, Woods reported to the Usenet group rec.games.playing-cards that the program had solved all but 14 of them, making the win rate for FreeCell almost 99.999% (compared to win rates of 75% for Baker's Game and 89% for Seahaven Towers).

In 2001, Microsoft released a new version of FreeCell for its Windows XP operating system. This version extended the number of available deals up to 1 million. The first 32,000 are the same as in earlier versions of MS FreeCell. The additional deals are the same as those in FreeCell Pro, Pretty Good Solitaire, and other programs. Eight of those one million are impossible.

* Why doesn't Microsoft FreeCell always tell me when I have lost?

The Microsoft program flashes the blue title bar at the top when you have exactly one available move. It puts up a text message only when you are completely out of moves (this can only happen when all of the freecells are full, there are no empty columns, no cards can go to the homecells, and no card can be moved from a freecell or the bottom of a column to the bottom of another column). The same is true of FreeCell Pro and probably other versions of FC. But it is possible to be hopelessly lost, but always able to make at least one move. A common situation is to have, for example, a red five on a black six at the bottom of one column, and the other black six available at the bottom of another column. The red five can be moved back and forth indefinitely, but if no other moves are available, the player has lost. It would be possible for a program to be written to detect this situation, but there would always be slightly more complex situations which would not be detected. Championship FreeCell was the first FreeCell program I saw which detected many lost situations while a deal is in progress (Faslo FreeCell Autoplayer, discussed later, can also do this passively; FreeCell Pro can do so on demand).

* Which deal is the hardest to solve?

Difficulty is a rather subjective question, so it is not possible to give a definitive answer. The difficult deals page contains a number of lists of deals which have been found difficult. From my own experience and reports from other solvers, I would nominate 1941 as the hardest solvable deal among the first 32,000. Another possible candidate is 10692 (in Windows XP or FreeCell Pro, try 80388). Besides the impossible deal number 11982, the most frequently asked-about deal is number 617. Although there are many harder deals, I suspect that 617 is the first really difficult deal that many players encounter when playing the deals in sequence. For some reason, about half the people who write asking for a solution without checking the catalog index (and please don't be one of them) are asking for a solution to 617. Worse yet, seven different people have written me to tell me that Brian Kraft's posted solution is wrong, and all of them were having trouble at the exact same spot, move 20 (51). The solution is correct; I wish I knew why it was causing so many problems (possibly because the trouble spot is a supermove?). The first really hard deal past the first 32,000 deals is probably 35254. I've had seven people ask for a solution or ask whether it is solvable (it is; the next impossible is past 100,000). Danny A. Jones suggests 57148 and 739671 as two of the hardest in the first million.

 7D AH AS TD 6C TC JH AC
 2S 4H 2C 3C TH 5H 9C 7H
 9H KH 3H AD 9D 8S JD 7C
 5C 4D 8C 6D QS 5D KS 7S
 9S 8D JC 6H 4S 3S QH 2D
 TS QD 8H QC 2H 6S JS KC
 3D KD 4C 5S

  Deal number 94717719

With solvers now having analyzed the first 100 million deals, a new candidate for hardest has turned up.  Shlomi Fish posted a solution to deal number 94717719 which was over 200 moves long, in which 7 spades are played to their homecell before any other aces are freed, and the entire spade suit is run while only two clubs and no red cards have been played to the homecells.  He later got it to 139 moves. Gary Campbell cleaned it up a bit, down to 119 moves.   Danny A. Jones used an older version of his solver to get it down to 92 moves.  Danny notes that it takes 40 moves just to reach the ace of spades, while many deals are already solved by that point:

#94717719 Danny A. Jones PRI solver  92 moves
13 6a 56 5b 52 51 57 5c 65 b6
78 7b 72 78 12 4d 74 a7 67 62
37 6a 64 c6 a6 1a 24 1c 12 17
14 a1 64 34 31 46 3a 32 36 36
a3 83 5a 5h 75 7h dh 7d 7h 42
87 d2 37 3d b3 83 8b d3 8d 8h
81 84 b8 38 78 18 4b 4h 1h b1
21 24 2b 2h 7h 27 2h 3h b3 43
47 42 48 4b a4 25 c8 2a 2c 2h
2d 28

* How are the deals numbered? Are those deals random or were they selected in some way?

The way computers create "random" deals is by using a number as a seed for a random number generator. The Microsoft version of FreeCell uses a number with a range of 1-32000 as its seed; the New Game (F2) function selects one of these at random.  You can also type in any number you choose yourself. There is a persistent urban legend that the deals are somehow constructed in reverse to make sure every one is solvable; this is not so. The deals are also not "preset" in the sense of being deliberately chosen (except for the deals -1 through -4 added later); they are the result of the algorithm Jim Horne used, and are as random as a computer can make them. The only way I know to get deals more random than a computer is to shuffle and deal an actual deck of cards. The actual C code used by Jim Horne is available, with Jim's kind permission. FreeCell Pro and a number of other programs for various platforms can produce the same set of 32,000 deals as in Microsoft FreeCell (and the same million as in Windows XP).  Horne's algorithm uses the Micrsoft C random number generator;  implementations of the dealing algorithm (which can generate the correct random numbers using a mathematical calculation) are available in over 50 different programming languages at the website Rosetta Code.  This algorithm can deal over 2 billion distinct numbered deals before the algorithm repeats.

* I have played hundreds of the deals randomly and started keeping a log by game number. But I notice that I never seem to win one twice. Does the program automatically turn up deals which have not been won?

No. The Microsoft program does not keep track of deals which have been played (whether won or lost). The New Game (F2) function picks deals entirely at random. If you have kept track over 200 deals, there is still a 53.62% chance of seeing no repeated numbers (if selecting from 32,000 deals). For 400, the chance drops to 8.2%; for 600, to 0.35%; for 800, to 0.004%. So if you continue to keep track, you should eventually see a repeat if you play enough.

* How can I get the solution to a hard deal I can't solve?

Check the index of the catalog of over 425 solutions (both the index and the catalog are in numerical order) to see if the solution you are looking for is there. It contains nearly all of the hardest deals. Gary Campbell's solver, now built into the Faslo FreeCell Autoplayer, can often provide reasonable solutions to deals (more on this below). I acted as a volunteer solver until July 2, 2003.  I am no longer doing so.

There is now a complete set of solutions to the first 1,000,000 deals (except for 11982 of course) on a new site based in Latvia, run by a gentleman named Yuri Bortnik (he replied right away when I asked about the site). The solutions all appear to be quite short, and the interface is very clean -- two clicks get you any solution up to 32000, and higher deal numbers can simply be entered in a search box. Yuri says that the "solutions are generated by computer. But a special human-friendly algorithm makes these solutions very sequential, logical and short of course." His longest solution is 53 moves, for deal 29596. Solutions are available in standard notation, or in a more detailed descriptive form. A very impressive job and a well-designed site. He has also added some stats on the first 64,000 deals, including a list of 0- and 4-freecell deals.

* Why am I finding deal number xxxxx difficult when it isn't on any of the lists?

Since a large number of people start at deal number 1 and work their way up in sequence, most of the lists of "difficult-to-solve" deals are bottom-heavy, with lots of low-numbered deals. One of the few lists which covers the whole range of 32000 is from Dave Ring's Internet FreeCell Project, but blocks of 100 were assigned randomly, and a deal may not have been reported as difficult there because the solver who got that block was an expert solver, or just didn't bother to report which deals he/she found difficult. So a deal may be very difficult even if it doesn't appear on any of the usual lists.  Difficulty is also somewhat subjective -- two solvers will not necessarily find the same deals hard. Most lists are compiled by one person or group, and most of those people/groups haven't tried every deal. There are some obvious things (particularly depth of aces and other low cards) to look for, but the best way I've found so far to objectively measure difficulty is to determine how many freecells are needed to solve a particular deal (FreeCell Pro is equipped to do this). FC 11982 requires five freecells to solve (i.e. it is impossible with the standard four freecells); only about one deal in 150 is difficult enough to require the standard four (most of these appear quite difficult to human solvers, so it seems like a reasonable measure). Surprisingly, it's only a little harder to solve many deals with three freecells rather than four, and FCPro lets you do this. Most deals (about 79%) require two freecells or fewer; any deal requiring at least three freecells is well above average in difficulty.

* Has anyone found a solution for Freecell xxxxx? It seems awfully difficult because of the remote positions of the aces.

The depth of aces is a very weak measure of difficulty. 14652 (one of the deals this question was asked about), despite 16 cards covering the aces, is only a little above average in difficulty, though it's pretty hard to solve with two freecells. The average deal has slightly more than 11 cards (576/52 = 11.077) covering the aces (possibly including other aces). Although the impossible 11982 has 22 cards covering the aces (close to the maximum 24), probably the hardest of the 31,999 solvable deals, 1941, has only 14, less than some of the zero-freecell deals. 617, which is nowhere near as hard as its reputation (and much easier than 1941), has 20, the same number as 164, which is a zero-freecell deal. The 69 zero-freecell deals average 8.51 cards covering the aces, only a few positions shallower than average.  52583 has all four aces available immediately, but requires the average two freecells to solve.

Pretty Good Solitaire includes a game called Challenge FreeCell, in which all of the twos and aces are automatically dealt to the tops of the columns (twos in the four leftmost columns, aces in the rightmost -- I would have done it the other way around). This makes the deals slightly harder to solve, but almost all of them are still solvable. Danny A. Jones ran an analysis in which he modified the million XP deals in the same manner. Only 14 deals out of a million are impossible (45813, 46589, 54150, 108905, 465251, 479573, 501129, 510749, 514842, 541924, 685515, 798261, 845934, and 855773. His solver found 846878 intractable. When he reversed the positions of the aces and twos (aces in columns 1-4), 19 deals were unsolvable (including some of the same deals as before, indicated in boldface) and 3 intractable (including 855773 which is impossible the other way). PGS's Super Challenge FreeCell combines this modified deal with KingOnly rules (only kings may be played in empty columns -- see the question below about variants); most of the deals are still solvable. Danny ran 40,000 deals, finding 56 impossible and 28 intractable. Even with two or three freecells, Challenge FreeCell is only slightly harder than regular deals. With three freecells, Danny A. Jones' solver found only 250 impossible deals (with 3 intractable) with the twos and aces in the first eight positions. With two freecells, there are at least 24,161 solvable deals. With one freecell, however, his solver found only 3,785 solvable deals, and there are only four Challenge-modified deals (7079, 17873, 20393, and 20918) solvable with zero freecells.

* I have a streak of xxxx wins in a row and have won xx% of the deals I have played. How does that compare to other players?

Since the statistics in Microsoft FreeCell can be easily altered, and you can escape from lost deals without recording them, there seems little point in collecting records on the honor system. (Unless you erase statistics and start over, your overall winning percentage may be a better indication of how quickly you became good at FreeCell rather than how good you are now. The more deals you play, the more slowly your overall win rate will change. Once you have played thousands of deals, it takes much longer to push your average up very much.) If you're really interested in comparing yourself to other players, try NetCELL, an on-line (Java) version of FC with has lots of features in addition to keeping records of streaks, win percentage, and average time. A few years ago, NetCELL moved to a new server, and now holds free on-line tournaments daily (with a prize tournament each weekend). Using NetCELL for comparison, I would say that you need to be winning 98% of FC deals on the first try to be considered a top-notch player. 90% is a reasonable level for a good player.  More than 100 streaks of over 1000 have been recorded on NetCELL, but I would consider anything over 100 excellent in any standard version of FreeCell. My own best streak of 119 straight made it up to 91st place on the list of longest active streaks in December of 2012.  Note that NetCELL does not allow undos, so getting long streaks is harder than in standard MS FreeCell, where you can fix a one-move mistake.

The all-time record on NetCELL is 20,994 by a player called Ki; the current best is 20012 by PudongPete.  The previous record on NetCELL was 19,793, set by Bob K., a retired chemist in the Atlanta area (under the name rgk5). He previously had a record of 12,856 (now fourth-best) under the name rgk1, which had shattered the old record of 5301 by a player going by the name Michelangelo. Bob started playing around 1996, and has also had ten other streaks of over 2000 wins. He did not record the deal which ended his streak of 12,856, but says that the loss was due to a simple mistake -- putting a red three on its homecell instead of on a black four, and having nowhere to put a black 2 which was in a freecell.  A streak of over 1300 is needed to make the top 100 all-time.

* Are all of the solutions in the catalog correct?

Adrian Ettlinger ran the entire catalog through FCPro's replay function, and all of the errors it found have been corrected. There should be no incorrect solutions. We frequently get claims of errors, but none of these has turned out to be correct except for one report of a solution which was missing a couple of moves at the end.

* Why won't you post every new solution submitted?

Because there isn't room for solutions to all 32,000 deals. Most of them aren't interesting anyway: with reasonable experience almost anyone can solve about half of the deals on the first try. Actually we aren't currently soliciting any submissions of new solutions, and have removed some of the easier deals (like most of those from 11 to 52, leaving 1-10 for beginners). Mainly the catalog is intended to contain solutions to very hard deals, although solutions to a few deals using zero and one freecells are included, as well as curiosities like 52-card flourishes. For quite a while we didn't add any new solutions, then started adding solutions to deals requested more than once.  Now we are adding no new deals, since there are complete catalogs of all 32,000 deals (and at least one catalog of the first million, as described above).  The catalog on our site is now basically a historical artifact.

* Why won't you post improved (shorter) solutions in the catalog?

There are several reasons. First of all, it would mean extra work for me, and wouldn't do much for anyone except the person sending in the improved solution, who would get to see his/her name there. (For some reason, 617 is the champion here too -- I have received quite a few submissions shorter than the catalog solution, but I have even shorter ones in my files, with as few as 44 moves, which I never bothered to publish). But the catalog was never supposed to be a competition; the main purpose is to give solutions to hard deals so that people who are stumped by a particular deal can look up a solution. For that purpose, any decent solution will do. Another point is that minimum-length solutions are likely to be tricky rather than elegant -- solid technique will usually not help you find shorter solutions; playing around and cutting corners may. One of the reasons I stopped playing Championship FreeCell (a competitive version no longer available) is that if someone was the first to post a 2-freecell solution to a particular deal, and someone else posted a shorter solution, the original poster lost all credit whatsoever for having posted it -- so there was little incentive (from a competitive point of view) to investigate and find the minimum number of freecells needed to solve a particular deal for which no solution had been posted -- it was better to steal deals from someone else, especially if they were ahead of you in the rankings. Championship FreeCell also counted every individual card move in determining shortest solutions, which discouraged long sequence moves and further encouraged loose play such as moving every possible card to the foundations.

Until recently, little was known about the shortest solutions for deals. Danny A. Jones has used his various solvers to look for very short and minimal-length solutions for deals. With his standard Pri-DFS (prioritized depth-first search) solver, he originally found that all of the first million deals (except of course for the eight impossible deals) can be solved in 64 moves or fewer, using autoplay and supermoves as defined in MS FreeCell and FreeCell Pro. With his BFS (breadth-first search) and recursive-search Pri-DFS solvers, he later reduced this to only four deals for which he has not been able to find a solution of 50 moves or less; the longest is 57148 at 54 moves, followed by 739671 at 53 moves, and 255317 and 526267 at 51 moves each. When he extended his search to 25 million deals, all solvable deals could be solved in 66 moves or fewer. Solution length does not automatically correlate with difficulty (1941 has a fairly short solution), but most of the deals with the longest solutions are quite hard. For most deals, the solutions from his recursive solver are often considerably shorter than this at the price of memory and execution time. Danny was thinking at one point of creating a web site to post short solutions for FreeCell deals.

His BFS solver can sometimes (but not often, because of memory limitations) find (probably) shortest solutions for standard four-freecell deals. The caveat 'probably' is necessary because he uses suit-reduction as a shortcut and can't guarantee a shortest solution. As a simple example, his shortest solution for 1941 is 35 moves, only one move shorter than K. H. Rodgers' solution in the catalog, which was found by hand and dates back at least to 1997. For other deals, his BFS solver produces more pronounced results. The shortest solution is not definitely known for many deals: the shortest known solution to 617 is 41 moves (but can be shortened to 39 using full autoplay and supermoves). Using a combination of his solvers and with maximal safe autoplay (as in NetCELL) and supermoves (as in FreeCell Pro), he has found 213 deals which can be solved in under 20 moves. The two shortest, 15924803 and 17182509, are 13 moves each (even using the more limited autoplay of MS FreeCell). Searching into the higher-numbered FreeCell Pro deals, he has found five deals which his solver cannot solve in under 60 moves; the longest solution of these is 24515390, at 66 moves. His BFS solver also solves zero-freecell deals. He has found 21,725 probably shortest zero-freecell solutions for deals in the first ten million FCPro deals, plus an additional 24 deals later found by his Pri-DFS solver.

* Which deal is the easiest? Are there any deals in which all of the cards go automatically home at the start?

A deal where all of the cards go home at the start is easy to construct, but it is fantastically unlikely for such a deal to occur at random, since Microsoft FreeCell or FreeCell Pro only plays an available card to its homecell automatically when all of the lower-ranked cards of the opposite color are already on the homecells (except that a two is played if the corresponding ace is on its homecell); aces are always played when available. This is one version of what can be called safe autoplay. NetCELL uses a more aggressive rule, making all of the plays that MS FreeCell makes, but also playing an available card if both homecells of the opposite color are within two ranks of that card and the homecell of the same color and opposite suit is within three ranks. For example, in NetCELL 28865-5, the four of diamonds is played as soon as the three of diamonds, both black twos, and the ace of hearts are on the homecells. The reason for this is that the four of diamonds is not needed on the tableau to hold either black three, since both can go to their homecells as soon as they are available, and the black threes are not needed to hold the two of hearts, since it can also go to its homecell as soon as it is available. (NetCELL plays as many cards as possible under this rule as soon as the cards are dealt; MS FC and FCPro don't do anything until the player moves the first card).

In order for a deal to have all 52 cards go to the homecells at the start (or even after one play), every column would need to be in (nearly) descending order of rank. There are no automatic deals even in the 8-billion-plus FCPro deals. The 32,000 Microsoft deals include 69 deals which can be won using no freecells at all. The largest number of cards which go to the homecells at the start of any of these zero-freecell deals is six (including all four aces), in deals 9998 and 11987 (a zero-freecell solution to 11987, which is in the catalog, is unusually short, at 36 moves). It's possible to get quite a few more cards to the homecells with a minimal amount of moves in both deals, and these seem the two most likely candidates for the title of "easiest deal". Mike Dykstra found a one-freecell deal, number 8695, where seven cards go to the homecells at the start. Bill Raymond found another one-freecell deal, 27245, where eight cards go at the start -- ten cards would go if it used the NetCELL rule.

Bill Raymond wrote a program to search for FreeCell deals in which large numbers of cards go to the homecells on the first play (using Microsoft's autoplay rule). His search of the 32,000 Microsoft deals turned up no other eight-card deals, and only one other seven-card deal (22265) in addition to the deal (8695) previously found by Mike Dykstra. All three of these are one-freecell deals. Bill extended the search through some of the FreeCell Pro deals: The first nine-card deal is 270618; this requires two freecells to solve, but is fairly easy. The first 10-card deal is 2710330, a hard one-freecell deal. The first 11-card deal is 3060287, a very hard zero-freecell deal. If you're looking for an extremely easy deal, try 22350203, an 11-card deal which is very easy even with zero freecells (my solution is only 35 moves).

The first 12-card deal is 12172106, a medium-hard one-freecell deal. The first 13-card deal is 17332733, another hard zero-freecell deal. The first 14-card deal is 181627041, an easy one-freecell deal. The first 15-card deal is 143973501, a hard zero-freecell deal.

The autoplay rules used by NetCELL sometimes allow many more cards to be played initially. There are no large increases in the 32,000 Microsoft deals (deal 27245 plays 10 cards, and 2217 and 22265 play 8 each). The most extreme case Bill found is 1195233675, in which the simple Microsoft rule plays six cards to the homecells, but the NetCELL rule plays twenty-three! This is a zero-freecell deal, and might be the easiest in the entire 8-billion-plus FCPro deals. Another interesting deal found by Bill is 446806382, another zero-freecell deal, which plays only four cards using the MS rule but 16 using the NetCELL rule.

Joe McCauley independently wrote a program to count how many cards were autoplayed, and extended the search through the entire 8 billion-plus FreeCell Pro deals. He also checked to see how many cards could be played to the homecells if *every* possible homecell play was made (Joe calls this AllPlay): three of the 32,000 Microsoft deals (4196, 5319, and 27245) play 10 cards using AllPlay, with one other (27403) playing 9. Interestingly, 4196, 5319, and 27245 are all one-freecell deals, but 5319 *cannot* be won with one freecell if you play all ten cards immediately to the foundations! (Playing nine works, but either the three of diamonds or the four of hearts is needed for packing.)

Using the Microsoft rule, there are five deals in which 16 cards play to the homecells (2016704153, 3453036771, 4418013924, 5856288588, and 8110636965). The first deal to break 16 using NetCELL rules is 1000572852, which plays 17 cards (only 5 in MS) -- despite 17 cards played and a whole column emptied, it cannot be solved with zero freecells, though it's not hard with one. 4418013924 plays 19 using the NetCELL or AllPlay rules. Using the NetCELL rules, two other deals play 19 cards (2178166022 and 2587385892), well short of the deal mentioned above which plays 23. Using AllPlay, three other deals play 23 cards (2587385892, 4931624547, and 7372172513) -- the last two play only four and six respectively under both MS and NetCELL rules. But two deals play more than 23 using AllPlay: 8305804964 plays 25 (only 5 under MS and NC), including all of the diamonds; 7841153263 plays 28, the only FCPro deal in which half the deck can be played at the start. Except for 1000572852, all of the deals mentioned in the last two paragraphs can be solved with zero freecells.

Some other curious statistics: slightly over half (50.15%) of all deals play no cards initially to the homecells (remarkably close to the theoretical value 19393/38675 = 0.50144). Another 30 percent (30.38%) play one card; another 14 percent (13.57%) play two (slightly less, 12.6%, with AllPlay); another four percent (4.38%) play three. Slightly over one percent play four or more; slightly over one in a million play ten or more using the MS rule (about four in a million in NetCELL and thirty-six in a million using AllPlay). It seems likely that the odds against all 52 cards playing automatically in a random deal are astronomically high; even if five percent of random columns are sufficently well-ordered, the odds are more than 25 billion to one against a complete deal playing automatically. Even with AllPlay rules, only 38 FCPro deals play 20 or more cards to the homecells.

Danny A. Jones has analyzed the effect on play if AllPlay is mandatory. If every card automatically goes to its homecell as soon as it can, most deals can still be solved, though play can sometimes be tricky. His solver analyzed the first 32,000 deals, and although the solutions are a little longer on average (52.94 moves, compared to 46.33 with safe autoplay), almost every deal can still be solved. The only exceptions are 1941 (perhaps the hardest of the 32,000 deals) and 11982 (which is impossible anyway). Danny later ran 1 million deals in less than an hour. Besides the eight deals which are impossible anyway, only two deals, 1941 and 98714 (a hard four-freecell deal), cannot be solved with AllPlay. The average solution length is 50.29 moves, with a maximum of 79 moves.

3. Variations and Related Games

* I'm getting awfully good at FreeCell. How can I make the game more challenging?

The only drawback to FreeCell is that about half the deals are pretty easy once you're experienced (of course you can try the lists of difficult deals). Dennis Cronin's NetCELL, an online Java version of FreeCell, has an ingenious algorithm to make deals harder or easier, by dealing more high cards at the tops of columns and low cards at the bottoms of columns (and vice versa). Originally the difficulty scale ran from 1 to 20, but he found that the higher numbers paradoxically were less difficult, and the maximum level available on the server is now level 12. There is a very competitive list (with hundreds of players), ranked by consecutive wins. The server also keeps track of winning percentage and average solving time for each player, and offers continuous tournaments (both long and short) every day with a mixture of variant games. When playing single games, in each game, you start at level 5 (pretty easy), and go up one level after every 10 consecutive wins, until you reach level 10 (random deals, with all cards equally likely at each location) after 50 deals. I once managed 119 in a row in the standard 8x4 game; in order to break into the top 100 all time, you need to win well over 1300 in a row!

If solving with four freecells is too easy, why not try two or three? This option is available in NetCELL, as well as several Windows 95 versions of the game, including FCPro and the defunct Championship FreeCell. The people at Championship FreeCell estimated that nearly all deals (about 99% judging from their first sample of 500 deals) can be solved with only three freecells, about 80 percent with two freecells, and perhaps 15 percent with one freecell (see section 5 for more precise statistics). Thomas Warfield's solitaire compendium package Pretty Good Solitaire, an excellent Windows shareware program with over 600 solitaire games (including FreeCell), includes the Solitaire Wizard, a system which lets you define your own games by setting a handful of parameters. It is simple to use this to set up FreeCell or Baker's Game with any number of freecells up to 8, and with variable column widths. I first saw these options in a shareware version of FreeCell for Windows 3.1, written in 1992 by Marc L. Allen. I expect it must still be available somewhere on the Internet, but I can't give you a current URL.  My copy doesn't run any more under Windows 7 Home Premium.

Another more challenging way to play is to allow only kings to be moved to empty columns (as in FreeCell's ancestor Eight Off, and related games such as Seahaven Towers). This means that empty columns cannot be used as extra freecells, and supermoves are impossible. Pretty Good Solitaire allows you to change the rules to allow this option, which PGS calls KingOnly. I think that KingOnly loses some of the flavor of FreeCell, and only slightly reduces the win rate.  Danny A. Jones has analyzed the 32,000 MS deals and found that only thirteen deals cannot be won using KingOnly: 617, 7477, 11982, 16129, 17683, 18192, 20021, 20630, 21491, 26693, 29230, 29377, and 31465. Nine of these are four-freecell deals (20021, 20630, and 29377 can be won with three); 11982 is impossible even under normal rules, of course. His solver does not reach a conclusion with 14292 or 23017. Eventually I ran a modified version of Danny's solver on the first million deals; this took 82 hours of computer time over a period of several weeks. Danny reprocessed the intractables, getting definite results for a few. In the first million deals, there are 518 impossible with KingOnly (including the eight which are impossible anyway) and 25 intractable.

An avid player wrote to me and asked for a solution to a particular deal. When I sent the solution and explained the notation, she replied that she was surprised to learn that you were allowed to move cards to the homecells manually. She had solved thousands of MS deals relying only on autoplay to get cards to the homecells. Danny A. Jones suggests this is actually an easy way to make the game slightly more challenging (we'll call it AutoplayOnly), and has analyzed its effect on the win rate. Amazingly, all but five of the 32,000 MS deals can be solved with autoplay only: in addition to 11982 which is impossible anyway, the deals which require manual moves to the homecells in order to be solved (even with the more sophisticated autoplay rules described above, as used in NetCELL) are 617, 1941, 4603, and 31465. Three of these are among the most frequently cited hard deals; 4603 is a fairly hard deal as well. Danny comments that this scenario makes his computer solver "act like it was pulling a fat rhino through fifty miles of quicksand." Later he did a full analysis of the first two million deals, finding 131 deals which can only be solved with manual moves to the homecells, with seven intractables and sixteen deals already impossible under standard rules. Of these 131 deals, 96 require four freecells to solve with standard rules; the other 35 can be solved with three freecells. None can be solved with two, so it appears that virtually all such deals are above average in difficulty. With the autoplay rules used by NetCELL, 50 more deals (48 of the impossibles and 2 of the intractables) can be solved with AutoplayOnly, leaving only 83 impossible and 5 intractable.

Maybe one reason 1941 is so hard is that it is the only solvable deal found so far which is unsolvable with both AutoplayOnly and AllPlay -- you have to make manual moves to the homecells to win, but you can't make all of them, and must choose the correct ones.

Since some of the deals which are impossible with either KingOnly or AutoplayOnly are often cited as extremely hard, searching for such deals by computer may be a way to generate lists of extra-hard deals, or at least candidates for extra difficulty. Since both KingOnly and AutoplayOnly make the game a bit harder, what happens if you use both options? Danny's solver says that 164 of the first 32,000 deals are now impossible (with 83 intractable). The list includes many of the deals usually regarded as very difficult.

Pretty Good Solitaire also has games called Challenge FreeCell, and Super Challenge FreeCell, described above in the question about ace depth. PGS also has variations of FreeCell for two and three decks.

100 Best Solitaire Games by Sloane Lee and Gabriel Packard (ISBN 1-58042-115-6), includes FreeCell and several variants, including Bonus FreeCell, a version of Eight Off with alternate packing (in other words, it is ForeCell with four extra freecells).  It's hard to see how adding four more freecells, even initially occupied with cards, makes the game better: the win rate may actually be 100%. There are also two games with half of the cards dealt face down; they are no longer what I would even call FreeCell; if the game isn't open, you're playing a variant of Klondike.

Filling the four freecells with the last four cards (as in ForeCell but without the KingOnly rule; empty columns may be filled as usual) is another way of making the standard game harder. We mentioned results found by Danny A. Jones in the earlier section on ForeCell; he analyzed the first million deals and found that 878,429 are solvable (121,566 are impossible, 5 intractable), a win rate of 87.8%.

* What is Ephemeral FreeCell?

I originally thought of this idea when I was playing 13-column FreeCell with no freecells: what if I had one freecell, but I could only use it once? 

This led to the general idea of playing with freecells that vanish after you move a card out of them; I call this version Ephemeral FreeCell. This has not been investigated much, but should work particularly well with wider tableaux.  There is lots of scope for experimentation with combinations of permanent and ephemeral freecells (you could also prefill all or some of the permanent ones). This feature is available in the FreeCell Virtuoso program, which is planned as a replacement for FreeCell Pro. Charlotte Morrison pointed out to me that the idea of one-use freecells appears in the Pogo game Rainy Day Spider Solitaire; it has also appeared subsequently in other casual/adventure solitaires, such as Mystery Solitaire: Secret Island. Not only does adding ephemeral freecells greatly increase the number of combination games, it adds some extra strategic thinking to the game -- when should I play a card to a permanent freecell, and when to an ephemeral one?

But the main reason I hope that ephemeral freecells might be such a useful device is that they could enable deals to be placed into many more categories of difficulty, using computer analysis.   At the moment, we can group standard eight-column deals into eight categories, based on the minimum number of freecells each deal can be solved with (0 through 7).   We can say that a deal is very hard if it can be solved with four freecells (but not 3), and hard if it can be solved with 3 but not 2.  But we don't have an easy way to distinguish between, for example, the difficulty of deals like 1941 or 10692 with run-of-the-mill four-freecell deals.  But I imagined that a FreeCell solver with the ability to analyze Ephemeral deals might make it possible to determine that some four-freecell deals can be solved with 3 reals and 1 ephemeral, or even 2 and 2.

I asked Danny A. Jones for help, and he has begun adapting his solver to handle Ephemeral FreeCell.  Danny did a run (on August 11, 2012) of the first million MS deals, using three permanent freecells and one ephemeral one.  Besides the eight deals known to be impossible with four freecells, there are only four more which cannot be solved if one of the freecells is ephemeral: 255317, 412030, 707659, and 888541.   I have done some more runs of a million deals of various scenarios using his solver.  In the scenario with two permanent and two ephemeral freecells, there are only 30 additional impossibles.  One permanent and three ephemeral is a little harder: 58 of the first 32,000 and 1932 of the first million are impossible.

What if all of four of the freecells are ephemeral?  This is somewhat harder work for Danny's solver: it took 16 hours to process the first 32,000 deals, and 272 of them were intractable.  25484 of the deals, just under 80%, were solved, with 6244 definitely impossible.   So four ephemeral freecells is just a hair easier than two real freecells, but there's surprisingly little correlation between the impossible lists for 8x2 and 8x0e4: quite a few deals are solvable one way but not the other.   The first four 8x2 impossibles (1, 6, 21, 25) are all solvable as 8x0e4; the reverse is true of 4, 9, and 12.   32 is the first deal impossible both ways.

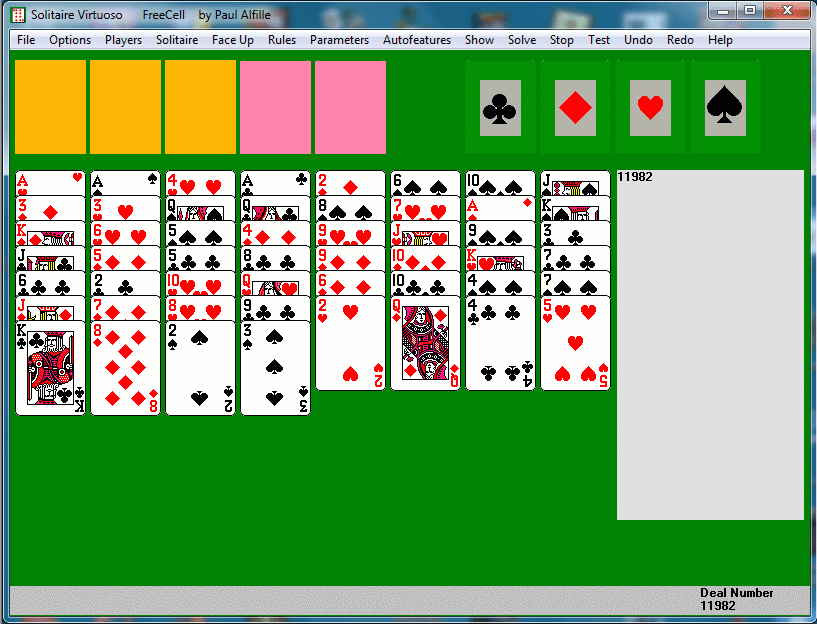
We can also look at the deals impossible with four freecells.  Danny determined that all eight of the 8x4 impossibles in the first million MS deals can be solved as 8x4e1.  Below is a screenshot of 11982 about to be played using 3 real (orange) and 2 ephemeral (pink) freecells.  A full solution is:

11982    8x3e2
 2d 2a 2b 2c 2e 78 28 4h 32 43
 23 12 42 a4 1a 14 c4 12 b8 32
 1b 17 35 b1 3b 31 35 a1 74 7a
 73 71 d3 84 8h 87 82 e2 b2 83
 85 8b 86 b8 68 6b 68 b6 38 58
 56 51 51 63 61 61 43 42 4b

* Can I play with a different number of columns?

Yes (this can also be done, of course, in a hand-dealt game with real cards). Playing with various numbers of tableau columns goes back to Paul Alfille's original version of FreeCell on PLATO, which allowed for every combination from 4 to 10 columns and 1 to 10 freecells (some of these are either virtually impossible or ridiculously trivial, though many players like the easy games either for relaxation, or as variants to be played very fast). We will use NetCELL's notation MxN to indicate a game played with M columns and N freecells (e.g. 10x2 is ten columns of 5 or 6 cards and two freecells). Several other computer versions allow for changing the number of columns, including Marc L. Allen's 1992 version, which allows between 6 and 10 columns. NetCELL has a large assortment of variant games from 4 to 13 columns wide, with as many as 10 freecells for the extremely narrow games:

freecells
columns 0 1 2 3 4 5 6 7 8 9 10
   13   * * * *
   12   * * * * *
   11   * * * * * *
   10   * * * * * * *
    9   * * * * * * * *
    8   * * * * * * * * *
    7     * * * * * * * * *
    6       * * * * * * * * *
    5         * * * * * * * *
    4           * * * * * * *

The game is much easier with nine or more columns: Danny A. Jones has analyzed games with nine columns or more and found that all 32,000 of the standard Microsoft deals are solvable with nine columns, even with only three freecells (in the first million deals, there are 19 impossible deals with three freecells and none with four freecells). With ten or eleven columns, most games are solvable with one freecell and almost all with two. With twelve or thirteen columns, most games are solvable with zero freecells and almost all with one. There are no impossibles in the first million deals at 10x3, 11x3, 12x2, or 13x2.

We now have some results for Ephemeral FreeCell.   The thirteen-column game is winnable almost 95% of the time with no freecells (there are 51,531 impossibles in the first million).  With a single ephemeral freecell, only 29 deals are impossible (none in the first 32,000: the first one is 35227).   If the single freecell is permanent, there are only five impossibles: 100730, 196724, 340351, 622692, and 680565.  All of the first million deals are winnable with 13x1e1, and even with 13xe2.   The twelve-column game is very winnable too: there are 148,158 impossibles with no freecells, only 956 with a single ephemeral, and 394 with a single permament freecell.  All of the deals are winnable as 12x1e1.

Using less than eight columns makes the game more challenging. Danny A. Jones' solver finds that there are at least 31,641 solvable 7x4 deals (seven columns and four freecells), so that game is slightly harder than the standard eight-column game with three freecells (8x3). What about combining the variants, playing with seven columns and three freecells? Of the 32,000 7x3 deals, at least 25,285 can be won; this is approximately as difficult as the standard game with two freecells. It is possible to play with six or even fewer columns, but the games become extremely difficult unless more than four freecells are allowed. A summary of win rates for all reasonable combinations of columns and freecells can be found below in the statistics section. You can scan the NetCELL score page to see some results from real players; good games which can still be won most of the time are 6x5 or 6x6, 5x7 or 5x8, and 4x10. The NetCELL stats may vary quite a bit from our calculated win rates, because of the effects of the NetCELL difficulty algorithm, especially in variants with larger numbers of columns.

* Is it possible to win without using the freecells?

Yes, but very rarely. Remember that cards can only be moved one at a time unless you have enough freecells or empty columns to move sequences, so a zero-freecell deal means, among other things, that you can never move more than one card at a time unless you can clear out an entire column, which will allow you to move two-card sequences, etc. (see the discussion of supermoves below). Wilson Callan had received several claims of deals which could be won without using any freecells at all (even temporarily during sequence moves), but we were unable to verify any of these reports. When the Don Woods solver used in FreeCell Pro was modified to allow zero freecells, the solver contradicted every claim received of a win without using freecells. Under the strict conditions of zero-freecell play, it is surprising that any deals can be solved, but remarkably, it turns out to be possible to win roughly one out of 500 deals with zero freecells (my solution, found by hand, to 1150 is posted in the solution catalog). A complete analysis of the 32,000 standard deals using four different solvers shows that 69 are winnable with zero freecells:

164, 892, 1012, 1081, 1150, 1529, 2508, 2514, 3178, 3225, 3250, 4929, 5055, 5152, 5213, 5300, 5814, 5877, 5907, 6749, 6893, 7018, 7058, 7167, 7807, 8355, 8471, 8961, 9998, 10772, 11863, 11987, 12392, 12411, 12676, 13214, 13464, 13532, 14014, 14624, 14826, 15140, 15196, 17772, 17871, 18026, 18150, 18427, 19951, 20533, 21657, 21900, 22663, 23328, 24176, 24919, 25001, 25904, 26719, 27121, 27853, 28856, 30329, 30418, 30584, 30755, 30849, 31185, and 31316.

Playing with no freecells makes the game a much harder form of the standard solitaire Streets and Alleys, with packing in alternate colors, instead of packing regardless of suit. It's actually much more likely, when playing with zero freecells, to have no moves at all from the initial position. In over 4% of deals it is impossible to make any moves at all without any freecells (Danny A. Jones found that 1,325 of the first 32,000 and 42,055 of the first million are blocked at the start; the first few are 1, 23, 25, 28, 46, and 51). Dozens of people have written claiming to have solved other deals without using the freecells, but invariably they are playing with Microsoft FreeCell and are using the freecells temporarily for moving sequences. If you really want to play without freecells, you can do so with FreeCell Pro.

Danny A. Jones says that the hardest deal he has ever encountered is the zero-freecell FCPro deal 1003256. He says, "It's guaranteed to quickly age manual solvers and turn computer solvers into memory hogs. It goes against almost every optimization technique employed in my normal solver. Think of your worst case of reordering cards to align suits ... and then multiply it by 100+ for this deal! None of the solvers in FcPro could find a solution -- not even after I helped by providing the first 40 moves!" He also suggests playing 896777 without making any manual moves to homecells (65 of the first million deals are solvable this way; 8 more if autoplay takes effect before moving any cards).

With fewer than eight columns, zero-freecell wins become even rarer. Only one deal, 16110, out of the first 32,000 is winnable with seven columns and zero freecells (2,780 are blocked at the start, and 87,323 out of the first million). The overall win rate appears to be about 1 in 100,000; there are 30 winnable 7x0 deals in the first three million FCPro-numbered deals. With six columns and zero freecells, no winnable deals have been found in the first ten million FCPro deals.

Adding one ephemeral freecell to the eight-column game makes 902 of the first million deals solvable (a few of these are 58, 104, 105, 116, 150, and 163).

* Why is it required to use freecells or empty columns to move sequences?

Because the way the game, and most of its relatives (Penguin is a notable exception), were designed, is that cards can only be moved one at a time. A variation where a sequence of cards can be moved as a unit, regardless of the number of freecells available (though freecells can still hold only one card at a time), is sometimes called Relaxed FreeCell. Danny A. Jones has analyzed the 320 deals out of the first 25 million FreeCell Pro deals which are impossible under standard rules. Amazingly, all but four of them can be solved in Relaxed FreeCell, including 11982. The deals which are still impossible are 2607073, 12421023, 18667482, and 24121426. Since the win rate of the standard game is already extremely high, it does not seem necessary to make the rules any easier (although solving the impossibles like 11982 using relaxed rules is sometimes quite challenging).   Here is a solution to 11982 using relaxed rules; moves followed by asterisks are sequence moves for which there are not enough freecells in standard rules:

11982 (solved with 4 freecells but relaxed rules)
4a 4b 41 4c a4 54 3a 3d b3 d3
8b 82 83 53 c5 8c 8d 81 31* 31
43* 48 24* 25 ch 7h 72 87 d8 18*
1c 17 15 16 1d 12 b5 25 21 24
2h 72 7a 72 34 d7 37 c3 63 51
5h 56 52 52 65 61 67

Many people enjoy playing Relaxed FreeCell with zero freecells (most are unaware that they are not following the standard rules, resulting in many false reports to us of additions to the zero-freecell list (previous question)). Danny has also analyzed the first 32,000 deals using zero freecells and relaxed rules. There are 1785 deals solvable under these conditions (the first few are 11, 38, 54, 56, and 58).

* Is it possible to get all 52 cards to the homecells at once?

Yes. While I was participating in Dave Ring's project, I noted that some deals ended with 40 or more cards going to the homecells at the end of the game (called a flourish, cascade, or sweep -- the latter term coming from peg solitaire). The best I managed was 47 cards. George W. Edman discovered a number of deals on which he could end with a 50-card flourish: 7329, 7851, 15824, 23600, 26963, 31126 (found by Carol Philo), and 31637. Edman's solution to 7851, remarkably short at 35 moves, is found in the solution catalog. Since the standard version of FreeCell plays aces automatically to the homecells as soon as they are available, these deals depend on having two aces buried at the bottom of the same column, and arranging the remaining cards into sequence before uncovering the last two aces. But in March 1998, Andy Gefen found the ultimate: a 52-card flourish. After noticing that deal number 18492 had four aces at the bottom of column six, he realized that if he could get all of the other cards in order without moving the seven of diamonds which covers the aces, he could achieve the 52-card flourish! He was able to do so after considerable effort, and his solution is now available in the solution catalog. Dave Leonard later found a second 52-card flourish, 22574 (with a different arrangement of aces), and a 51-card flourish, 765. Brian Barnhorst found a third 52-card flourish, 7239, Dave found a fourth, 23190, and Kenneth Goldman found a fifth, 16508. All of the solutions to these 52-card flourishes are found in the catalog. Ben Johannesen found five more, 9993, 10331, 12387, 17502, and 27251. Jason A. Crupper found 18088, and then used Jim Horne's dealing code to write a program to search the 32,000 standard deals for more candidates. He found six more for which he was able to find solutions: 7321, 8536, 16371, 28692, 29268, and 29640. This brings the total to seventeen. Jason found two other possibilities, but writes: "14150 and 26852 have the right setup of aces, but also present extreme strategical difficulties, enough that I suspect that they are unsolvable, in the same way that 11982 is unsolvable". Danny A. Jones's solver confirms that those two deals are impossible as 52-card flourishes.

Deals from other programs have not been examined in detail for 52-card flourishes, but Scott Kladke found the NetCELL deal 10904-8 which can be solved fairly easily as a 52-card flourish.

Later, Jason, using a new program he calls Flourish Explorer, extended the analysis through the first million deals, and found a total of 435 candidates for 52-card flourishes. Danny's solver has found solutions for 354 of those; 19 are impossible and 62 are so far unsolved. The search for candidates is very fast (Jason searched 100 million deals in 159 seconds, making a search of the entire 8 billion deals possible in about 3 hours), but the process of looking for actual solutions is very slow (over 17 hours for the analysis of the 435 candidates). Danny's solver also found a solution to 7239 using only three freecells.

A related variation, which does not depend on any special arrangements of the cards, is to play without moving any cards to the homecells (foundations), trying to arrange the cards in four ace-to king sequences on four of the empty columns. (This idea may have come from the solitaire Spider; it also can be used in Yukon and other games). This Spider variant is very difficult, and I do not know what percentage of games can be solved in this way. FreeCell Pro now allows you to play the Spider variant, but you cannot play the Spider variant in the Microsoft version, or any other version where autoplay is automatic and cannot be turned off. The Warfield and Allen programs mentioned above both allow it, as do some other programs.

* Can a card be played once it has been placed on a homecell?

No. In the standard form of the game, cards which are played to the homecells must remain there. Some variations of solitaire (e.g. Giant, a variant of Miss Milligan), specifically allow cards to be played from the foundations back to tableau columns (in English solitaire parlance, this is called worrying back). It doesn't make sense in games such as Baker's Game which pack in suit, but there's no reason why it couldn't be allowed as a variant in FreeCell.  Some FC programs allow worrying back as part of the standard rules; Solitaire Virtuoso provides it as an optional rule. Worrying back has a very small influence on the win rate, at least in the standard four freecell game: Tom Holroyd did some computer analysis and found 11 deals (impossible with the standard rules) that can be won by worrying back at least one card from a foundation back onto an occupied column (11982 is still impossible, though).   Danny A. Jones extended the analysis up to 100 million, increasing the total to 69 deals winnable only by worrying back:

(Holroyd) 4266168, 6332629, 7334559, 8381178, 10784666, 11953120, 13380013, 14194581, 15995200, 18739641, 19231830, (Jones) 19617733, 20001314, 24150534, 24795893, 26461140, 26960143, 27437151, 27616230, 30871801, 33293110, 33613814, 33900707, 34640348, 35784277, 40795834, 41445789, 45179955, 47883810, 48820590, 48830158, 49229215, 50279472, 50369429, 50532958, 50589757, 51869627, 53102422, 53126087, 53687601, 58996156, 59619214, 60555498, 61300229, 61830786, 62331953, 62641958, 63379066, 63478203, 64929238, 65924723, 66766350, 68311834, 70306173, 72865887, 74736875, 75265810, 78986182, 80505989, 81912256, 82943794, 85627209, 86265437, 89238318, 89819335, 90320629, 90801896, 95048417, 95464480

Here's a neat solution by Danny's solver, in which diamonds are worried back three times to solve number 47883810 (D indicates a move from the diamond foundation pile):

#47883810      49 moves
2a 3b 7c 17 41 34 23 2d 21 2h
a1 7h 7a 72 7h 74 D4 b4 8b 87
a8 D8 D4 74 27 32 dh 82 87 3a
37 c3 8c 27 6d 68 26 38 62 a3
26 43 52 56 45 48 4a 42 14


* What are some other solitaires closely related to FreeCell?

In the brief section on history, we mentioned Baker's Game, the in-suit relative of FreeCell, as well as much older predecessors like Eight Off. Baker's Game and FreeCell are the two most interesting games, in my view, since they allow any card to be moved to an empty column, so that the emphasis is on building sequences on the tableau, rather than moving cards to foundations as quickly as possible. But two other modern variants of Eight Off are also worth mentioning:

(1) Seahaven Towers, invented by Art Cabral, which resembles Eight Off, except that there are ten columns of five cards each, with the two remaining cards dealt into two of the four available freecells. This first appeared as a Macintosh game, but versions for Windows (and probably other platforms) are easy to find. Don Woods' solver estimates the win rate to be slightly over 89%.  Mark Masten ran Woods' solver for 15 million deals, with 13,397,816 wins (89.32%) out of 15 million. Much of the game's difficulty comes from only being allowed to move kings to empty columns; if the KingOnly rule is waived, the win rate jumps to over 98%. Using Tom Holroyd's Patsolve solver, the first 32,000 MS deals (dealing cards in the same order to ten columns instead of eight) were analyzed with both rules. Under standard KingOnly rules 28,564 deals are winnable (89.26%); with any card playable to an empty column 31,502 deals are winnable (98.44%).

The help file for the original Seahaven Towers mentions a harder variant (which is not implemented there): eight columns of six with the four remaining cards dealt to all four freecells; this is identical to ForeCell except that the tableau columns are packed in suit.  Danny A. Jones has analyzed this variant and found that only 3,382 deals are winnable out of the first 32,000 MS deals; in 1,276 deals no moves at all are possible.    Solvitaire also analyzed this variant, giving a win rate of 10.56% on a sample of 10 million deals.   It's also the same as Eight Off with four freecells (all initially filled) instead of eight: Mark Masten analyzed a million deals with similar results.

(2) Penguin, invented by David Parlett, and found in several of his books (Teach Yourself Card Games For One, published in 1994, is excellent, though now out of print, though easy to find used at a reasonable price). It also appears in a number of compendium programs, including Pretty Good Solitaire and Solitude. Penguin is an interesting variant of Eight Off, with seven columns of seven cards, and seven freecells. The first card dealt to the first column is the foundation base, and the other cards of the same rank are played immediately to the foundations as they are dealt, so that the last foundation card is buried at the bottom of the first column at the end of the initial deal. Sequences in suit can be moved from pile to pile without requiring freecells (i.e. Relaxed play); this is an exception to the usual rule in games of the Eight Off family. Mark Masten modified the Woods solver and ran fifty million random deals, estimating the win rate at 99.94%, slightly harder than FreeCell but slightly easier than Eight Off (99.88%).   He also gives win rates for a number of variants, including games with reduced numbers of freecells.

Thomas Warfield, author of Pretty Good Solitaire as well as other solitaire packages, has started a FC page which includes links to various sites, including ours, and a few of the computer versions of FC, including Warfield's packages FreeCell Plus (a Windows 3.1 package with FC and seven other related solitaires) and FreeCell Wizard (a Windows 95 package with 13 games and a modified version of the Solitaire Wizard, which allows players to set up games with a variety of rules variants). Both FreeCell Plus and FreeCell Wizard include Eight Off, Baker's Game, Penguin, and Seahaven Towers.

4. Computer Versions and Features

[The majority of this section is no longer being updated, and is retained for historical purposes.]

* Is it cheating to use computers?

Well, most of us are using a computer to deal and keep track of the deals, and FCPro can record solutions automatically. I think it is quite reasonable to use a computer to do things which would be impossible, tedious, or time-consuming to do otherwise. The Internet FreeCell Project took 110 people to finish; Adrian Ettlinger did more than 300 times as many deals alone using FCPro and his computer. The variable-freecell solver makes it possible to categorize random deals into six groups based on a rough difficulty rating, while leaving the more interesting task of actually solving individual deals to humans (all of the solutions in the catalog were found by humans without computer assistance).

* What are the minimum requirements for a good computer version of FreeCell?

The biggest flaw in Microsoft FreeCell is its dialog box which pops up every time you want to move to an empty column, asking if you want to move a single card or a sequence of cards. Moves of single cards to empty columns (when a move of more than one card from a column is possible) are very rare (the standard notation allows for this, but there is not a single instance of it in the catalog of over 400 solutions; I do not remember ever doing so when playing MS FreeCell), and it can always be done anyway in two steps by moving the single card to a freecell first, then to the empty column. This dialog box was eliminated very early in the development of FreeCell Pro, and most good versions of FreeCell either automatically move the maximum number of cards to an empty column, or use a drag-and-drop interface (though this is not as good an interface for FreeCell; NetCELL, strangely, allows drag-and-drop for single card movement only). Yahoo's version of FreeCell makes a different mistake -- it uses the selection method, but requires the player to select the top of the sequence to be moved, rather than simply choosing the column to be moved from (the rare cases where it is desirable to move part of a sequence to an empty column can also be handled by individual moves to freecells; a well-designed program would use alt-click, shift-click or control-click to select an exact partial sequence -- I have never seen this implemented). A first-rate program would allow the user to customize the selection method to behave exactly as preferred (FreeCell Pro allows the user to choose what action, if any, is taken on double clicks).

Every program should have autoplay of all cards which are safe to move to the homecells (preferably using the strong NetCELL autoplay rules described at the end of section 2); this speeds up play, especially at the finish. Being able to turn off autoplay completely is a nice optional feature. Poorly designed programs often make one of two errors: either not having autoplay at all, or playing every possible card to the homecells (as discussed earlier under AllPlay, this makes many deals much harder and on rare occasions impossible).

Every program should have selectable, numbered deals; part of the culture of FreeCell is the discussion of hard or unusual deals. Many versions of FreeCell, even non-Windows versions, have adopted the Microsoft deal numbers, at least for the first million deals.

FreeCell is an open solitaire -- the identity of every card is supposed to be visible at the start; this can be a problem with aces in particular if the cards are tightly packed together. Spreading the cards in each column far enough apart is the easiest way to do this (a large enough screen, as in FreeCell Pro, can easily hold the maximum possible 18 cards in a column). Microsoft FreeCell, which uses a very small screen, allows any card to be identified by a right-click, which momentarily displays the entire card (this is an easy feature to program and is quite useful in other games where there are often many cards in a column, where the spacing between cards in a column is automatically adjusted when it contains more cards than normal). Some programs use specially designed cards with extra suit indices on the upper right corner, visible even with minimal spacing between the cards. Some very bad versions of FreeCell give the player no way of identifying an ace which is covered by another card; this perverts the nature of the game, which is strategic planning without guesswork.

* What is FreeCell Pro? What can it do that most other programs cannot?

FreeCell Pro is a Windows version of FreeCell written by Wilson Callan and Adrian Ettlinger (available free at our site). FCPro was originally written in 1997 for the purpose of automatically recording solutions to interesting deals as they are solved by the user. The first version was a "tracking" program which ran while the user was playing the standard Microsoft FreeCell. It read mouse clicks, interpreted them, and correctly recorded solutions according to the standard FC notation devised by Andrey Tsouladze. In correspondence with Jim Horne, I asked about his algorithm for generating random deals, and he sent me the full C code for the dealing routine. There's nothing particularly tricky about it; a clever programmer could probably work it out by trial and error. But Jim kindly allowed us to incorporate the code into FCPro, and this allowed us to recreate the entire set of 32,000 deals of the Microsoft version (e.g. 11982 is unsolvable in FCPro too). Adrian later realized he could create a larger range of deals using a different storage type for the deal number, and eventially extended the range of deal numbers to over 8 billion. The first 32,000 are the same as those in Microsoft's standard version, and the first million are the same as in the Microsoft XP version released in 2001. Having Jim's dealing code and the FCPro solution-recording function allowed us to save (and later check) solutions to the standard deals. I used FCPro to record and send to Wilson dozens of my solutions to difficult or interesting deals.

The next big leap forward for FCPro occurred when Don Woods sent us the C code for his automatic solving program. He had used this to analyze one million random deals, and found that all but 14 were solvable. Adrian incorporated the code into FCPro, and added a function to allow a range of deals to be automatically processed. He also added some sorting routines to rearrange the eight starting columns according to various schemes; this frequently allowed the program to quickly solve a deal which otherwise proved difficult. Another feature in the program allows the user to select any number of freecells from 0 to 9 -- this works with both the manual play function and the automated solver. FCPro also includes a Next Game function (F5) which allows the deals to be easily played in sequence, a new Options menu which allows player preferences to be saved in the program registry, and a Custom Game function which allows any possible deal to be entered through a simple text file.  FCPro runs under all versions of Windows through Windows 11.

Most versions of FreeCell now have at least a million deals with the standard numbering.  I offer the following deal as a challenge: 80388.  It is solvable, but it is the most difficult deal I have yet found outside the first 32,000.

Since Microsoft FreeCell for Vista has now corrected its handing of supermoves, a few of the catalog solutions recorded with FreeCell Pro will no longer play back correctly in Microsoft FreeCell. In particular, when moving a sequence of four cards from a column to an empty column, when there is another empty column and one empty freecell, FCPro breaks it up into three separate two-card moves to match what older versions of MS FC did.

* What are some other programs which allow you to play FreeCell?

FreeCell Pro is now over 20 years old and is essentially moribund (no new versions appeared after 2002 ears and it is no longer being developed). A relatively new program is the Faslo Freecell Autoplayer developed by S.S. Reddi and Gary Campbell, which incorporates Gary's very strong solver. It has many of the same features familiar to FCPro users, including deal numbers up to 4294967295 which are compatible with MS FreeCell and FreeCell Pro. There are also new features not found in FCPro: its game playing function can detect losses up to four moves ahead of time, even when there are moves still available. FFA also has a Hint function which almost instantly suggests the next move (or two if desired) if the deal is still solvable; this was one of the most-requested features for FCPro, which was never implemented there. (Since the suggested moves come from the solver, they are always going to be good suggestions, unlike some other programs which merely suggest a legal move). You can use backspace to undo moves anytime, even after a loss is signaled. One of the coolest features (another FCPro suggestion never implemented) is that when the program signals impossible, you can backspace one move at a time until it signals solvable (no need to rerun the solver and click OK as in FCPro). Displayed solutions are much shorter and cleaner than those of FreeCell Pro, and incorporate multi-card moves. Solutions can be played through using the right (and left) arrow keys. Gary also notes that deals (and full or partial solutions) can be output to the Windows clipboard (and then to a text file) using the F9 key, and F6 reads a deal from the clipboard, so you can type a hand-dealt deal (or a deal from a non-MS-compatible program) into a text file, select, copy, and read into FFA for play and analysis. (The format is a little tricky; the best method is to save an F9 template as a text file and replace the layout text with the deal you want to input). The program can be downloaded and used for free, though donations to Gary for its development are gratefully accepted. This powerful program may become the new standard for FC analysis programs; at the present its major limitation is that it only handles the standard four-freecell game.  Gary's website includes a detailed tutorial.

Two other new programs with solvers are being developed in Java. Junyang Gu is developing a solver.  A group of students at Vrije Universiteit (Amsterdam, The Netherlands), led by their professor Daan van den Berg, are trying to use the results of human-played FreeCell deals to develop a solver.

There are quite a few packages for Windows which include FreeCell (and sometimes variants) among their many games. BVS Solitaire Collection is a large package of 435 solitaire games, with many powerful features, including an autoend function which tells you when you are stuck. Their version of FreeCell allows some of the rules to be changed, but does not appear to allow variable numbers of columns and freecells. The deals are numbered, but are not compatible with MS deal numbers. The program allows either drag-and-drop or select-source-and-destination movement interfaces.

Solitaire City is a program recently expanded to 13 games (53 including variants), including FreeCell, Klondike, and Spider. Their version of FreeCell includes seven game variations, six of which can be played against the clock to score points and compete against others (tables of the highest scores in each game are published on the website). The variants are standard, easy (similar to low levels of NetCELL where low-ranking cards tend to be dealt later), hard (the reverse, like high levels of NetCELL), and one, two, and three freecells. Because the competition is speed-based, the designer, Peter Wiseman, chose not to implement autoplay, and numbered deals are only available as a seventh variant. The deal numbers go up to 4294967295, and are compatible with MS deal numbers (higher numbers also match those of FreeCell Pro). Solitaire City includes a number of features, including autoend, a tutorial for each game, and a move hint feature which seems to give intelligent suggestions.

* Are there versions of FreeCell for Macintosh or other systems?

[This section was written many years ago and is obsolete.]

While there are probably at least a dozen in Windows, I know of a few versions for Macintosh: the first freestanding version was David Bolen's Super Mac Freecell (the old home page seems to be gone and the program may no longer be supported). Two newer versions I have not seen are a Dashboard Widget version by Daniel Erdahl, and an OS X version by Alisdair McDiarmid, which includes support for the first million MS deals (modified by Lowell Stewart). Several large packages for Macintosh also include FreeCell: Rick Holzgrafe's Solitaire Till Dawn (which includes FreeCell among its 40 games), Eric's Ultimate Solitaire (which includes FreeCell among its 23 -- also available for Windows 95), and Ingemar Ragnemalm's Solitaire House (which includes FreeCell among its 32). I have no access to a Macintosh, and have only seen Solitaire House and Super Mac FreeCell, both of which run on experimental Macintosh emulation programs. I have also not seen The Ace of Penguins, a Linux version by D. J. Delorie (Karl Ewald, who mentioned this version, says that it does not even support selectable deal numbers -- this is so easy to do, and so desirable a feature, that its absence in any version of computer solitaire is in my view inexcusable), nor versions of FreeCell available for Amiga, OS/2 (both of these links have unfortunately disappeared), and Clipper. Among the other Windows versions are the Windows 95 version Xcell. There used to be a version of FreeCell (and other solitaires) for Web TV, from Epsylon Games; this did not work well on an ordinary browser, and I received conflicting reports on how well it worked on Web TV. The site vanished entirely in 2001. A package which runs on a wide variety of platforms is a new edition of the Solitaire Antics package, called Solitaire Antics Ultimate, by Masque Publishing. The new edition, on CD-ROM, has over 200 games, including FreeCell, plus a very powerful game editor, and runs under Windows (95 through XP), Macintosh, Windows CE, and Palm OS (the latter two allow it to run on many handheld PCs).  Other packages available for both Windows and Macintosh are Burning Monkey Solitaire, which has 30 games including FreeCell [apparently no longer available], Solitaire Plus!, which also has 30 different games including FreeCell, and dogMelon's Classic Solitaire, available for Windows, Palm, and Macintosh (all including FreeCell, with varying numbers of games).

* Are there any handheld versions of FreeCell?

[This section was written in the pre-smartphone era: probably few if any of the devices below are still available.  Nowadays there are hundreds of versions for both Apple and Android phones, too many to even attempt to evaluate, or even list.]

MGA Entertainment has released a handheld FreeCell, selling for $15-16 retail. I wish I could say it was well done. The screen is tiny (about 49x42 mm), and is in color (but the suits are red and white and it is easy to mistake hearts for diamonds and clubs for spades). There are apparently only about 1000 different deals (the reason for this limitation is not clear), and they are not numbered. The interface is somewhat clumsy, requiring multiple buttons to be pushed for many simple operations such as moving sequences (the whole sequence must be selected with a roll up button) and moves from freecells other than the lefthand one (similar to keyboard notation). Only six cards per column can be displayed, and the roll up button must be pushed to view deeper cards. Another handheld version has appeared from Radica (about $20 retail), but this version is even worse than MGA's; it displays only four cards per column and uses a thumbwheel to scroll deeper in the columns.

There were also a number of FreeCell packages available for handheld and palmtop PC's including the HP, Psion and Palm Pilot. In fact there were at least three versions of FreeCell for Palm Pilots (all of them appear to have vanished): one from Electron Hut (this had the same deal numbers as Microsoft FC), another called Acid FreeCell from Red Mercury, and a portable version of NetCELL.  Microsoft made a version of the Windows Entertainment Pack (including FreeCell) for the Windows CE operating system, for $34.95. This ran on various handheld PCs (H/PC) such as the Hewlett Packard HP360/620 LX and Sharp Mobilon, but no longer seems to be available. Micah Gorrell wrote a free version of FreeCell for the Palm Pre; I'm not sure if this is still available. Gorrell later wrote an omnibus program called Solitaire Universe for HP Touchpads. This has free versions of FreeCell, TriPeaks, and Klondike (deal 3), and can be expanded to include more than 50 other games and variants.

I have also seen a countertop version of FreeCell (this is a touchscreen unit, similar to a video game, which can be found in restaurants and bars). The version I saw was called QuickCell, and is one of the games offered by Merit Industries' Megatouch XL unit (a bit pricey for home use, at $3195). Another touchscreen version of FC is found in the JVL Concorde 2 by J.V. Levitan Enterprises, Ltd.

ElectroSource International has published a version of the Microsoft Entertainment Pack (including FreeCell) for the Color GameBoy. Jeffery K. Hughes, the programmer for ESI's version, notes that the deal numbers in this version match those of the standard Microsoft Windows version exactly. Interplay published a package (written by Beam Software), Solitaire FunPak (about $20), for GameBoy and GameGear, with 12 solitaires, including FreeCell, but this now appears to be out of print. If anyone knows of other versions of FreeCell for video games (Nintendo N64, Sony Playstation, etc.), please let us know. It's been years since I played any video games (Intellivision and the original Nintendo), and I have no idea whether there are any other solitaire card games for them.

* What other computerized solvers exist?

Don Woods also wrote versions of his solver to analyze the related solitaires Seahaven Towers and Baker's Game; Mark Masten has modified these to analyze Eight Off and Penguin. Shlomi Fish has a solver available at his home page (it is written in C and runs on various platforms, including DOS). It has many features and can solve deals from FreeCell and a variety of solitaires related to FreeCell. A new solver by Gary Campbell, which originally ran as a command file under DOS, has recently been integrated into the Faslo program mentioned above.

There are a number of other FreeCell solving programs; none of those I have seen appear to be as fast or powerful as the programs mentioned above. Lingyun Tuo wrote a solver as part of his Autofree program. Luc Barthelet wrote a solving application (notebook) for the analysis package Mathematica. XCell also had a built-in solver (the links for these have all disappeared).

There are a number of unpublished solvers I know about. Danny A. Jones has a very powerful one, which he has used extensively to find solutions and win rates for this FAQ. His standard solver, running under Windows XP on a 1.8 GHz Pentium 4, can solve the first million deals in under an hour.

5. More Statistical Facts and Curiosities

* How often can I win?

Adrian Ettlinger, using Don Woods' solver with some extensions of his own, analyzed 20 million deals, starting with the standard 32,000 of the Microsoft version, and continuing on through deals numbered up to 20,000,000 (using the same random number scheme as Microsoft FreeCell, thanks to Jim Horne). This analysis was primarily carried out with the program FCPro, written by Ettlinger and Wilson Callan. Of the first 10 million deals, 130 are unsolvable in the standard four-freecell game:

11982, 146692, 186216, 455889, 495505, 512118, 517776, 781948, 1155215, 1254900, 1387739, 1495908, 1573069, 1631319, 1633509, 1662054, 2022676, 2070322, 2166989, 2167029, 2501890, 2607073, 2681284, 2712622, 2843443, 2852003, 2855691, 2923820, 3163790, 3172889, 3194539, 3217820, 3225183, 3366617, 3376982, 3402716, 3576395, 3595299, 3878212, 3946538, 4055965, 4207758, 4266168, 4269635, 4324282, 4334954, 4440758, 4446355, 4765843, 4863685, 4910222, 5046726, 5050537, 5086829, 5225172, 5244797, 5260342, 5401675, 5478410, 5611185, 5672090, 5817697, 6020049, 6099064, 6100919, 6234527, 6314799, 6332629, 6416342, 6749792, 6761220, 6768658, 6844210, 6895558, 6898316, 7035805, 7261039, 7334559, 7360592, 7400819, 7484159, 7497878, 7530003, 7536454, 7705172, 7748399, 7777900, 7795097, 7801943, 7814345, 7825750, 7863486, 7887312, 7923001, 7965413, 8000527, 8046431, 8076134, 8104908, 8105324, 8114984, 8119415, 8121228, 8237732, 8267373, 8354257, 8381178, 8527378, 8608154, 8712426, 8719444, 8736337, 9093368, 9110337, 9190487, 9222830, 9262134, 9414989, 9415104, 9435589, 9452398, 9626317, 9647001, 9660366, 9747437, 9771903, 9830419, 9855268, 9861848, 9917279.

Most notably, we verified the result of the Ring project: all but one deal (11982) of the 32,000 standard deals is solvable! No more unsolvables turned up for more than 100,000 more deals. Eight of the one million deals in FreeCell for Windows XP are unsolvable. Danny A. Jones has extended the analysis to 20 million using his own solver (of the first 25 million, 320 are impossible), and Ryan L. Miller (running Tom Holroyd's Patsolve solver in FreeCell Pro for more than 22 days of computing time, with some assistance from me, Danny A. Jones, and Gary Campbell) has extended it to 100 million. Of the first 100 million, 1282 are impossible, a win rate of nearly 99.999%, or about 1 loss in 78,000 deals.

In 2018, Theodore Pringle and Shlomi Fish completed analysis of all 8-1/2 billion FreeCell Pro deals, finding 102075 deals which were impossible, with no intractables.   Six of the deals are impossible with five freecells, but solvable with six.

A more difficult variant of FreeCell, as mentioned above, is to play with fewer than four freecells. Even with three freecells, approximately 99-1/3% of deals can be won (199 of the first 32,000 cannot be won with three freecells; Ettlinger also ran another segment of some 67,000 deals with a similar win rate). The deals below 1000 which require four freecells to win are: 169, 178, 285, 454, 575, 598, 617, 657, 775, 829, and 988. A full list is in the list of difficult deals page.

Based on analysis of the first 32,000 deals, we can also give some results for smaller numbers of freecells. With two freecells, the win rate is about 79-1/2% . It has been found, as a result of recent work by Shlomi Fish (following earlier work by Danny A. Jones), that 25,381 of the first 32,000 deals are solvable and 6,619 are impossible.  The last of these to fall was number 982, which was intractable for quite a while but eventually proved impossible.  Shlomi Fish and his colleague Jonathan Ringstad (who provided computing resources and support at the University of Oslo) have extended their analysis through the first 400,000 deals, finding 317,873 solvable and 82,126 impossible.  Only deal number 384243 has still proved intractable.  More details are available in the September 2, 2012 posting on Fish's blog.

With one freecell, the win rate is slightly less than 20% (at least 6289 of the first 32,000 are solvable) -- thanks again to Danny A. Jones and Shlomi Fish and their solvers for these results. The win rate for zero freecells (discussed in section 3) is about 0.22%.

The approximate win rates (per 1000 deals) for variant games with different numbers of freecells (across top) and columns (down left) are:

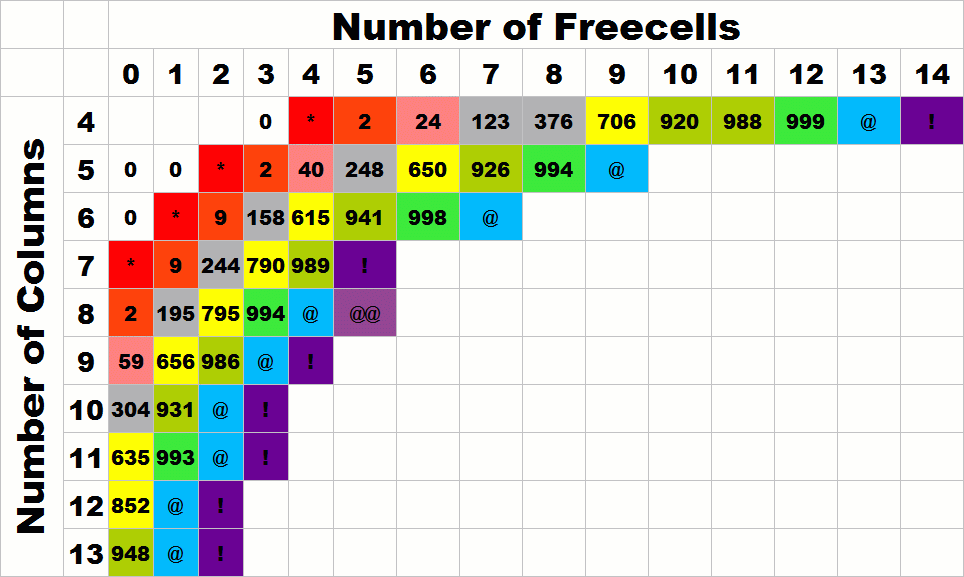
White boxes with zeros indicate variants where no winnable random deals are known.  Red boxes with asterisks have win rates less than 1 in 1,000.  Blue boxes with At Signs have win rates greater than 99.95%.  The lavender box with a double At Sign has a win rate greater than 99.9999999% (there are now six known random 8x5 deals which are impossible).  Violet boxes with exclamation points indicate that no impossibles have been found.

* How many freecells are needed to solve any possible deal?

At least seven, it appears. All of the 130 impossible deals in the first 10 million can be solved with five freecells, including of course 11982. I looked at a number of other constructed deals, including Hans Bodlaender's, the Microsoft joke deals -1 and -2, and others which have been posted at various websites and on Usenet newsgroups. All of them are solvable with five freecells. I was beginning to wonder if all deals were solvable with five freecells, when Adrian Ettlinger sent me a deal he constructed, which appears to be impossible with six freecells as well as five (confirmed with two different solvers). The arrangement of suits and colors is particularly fiendish. You can play this deal in FreeCell Pro by copying the lines below into a file and using the Custom Game option:

AE-Imp6
AC AD AS AH TD JD QD KD
6D 7D 8D 9D TH JH QH KH
6H 7H 8H 9H 2D 3D 4D 5D
2C 3C 4C 5C 2H 3H 4H 5H
2S 3S 4S 5S 6C 7C 8C 9C
TC JC QC KC 6S 7S 8S 9S
TS JS QS KS

Making extremely hard deals seems to require such effort that I suspected that every one of the 8,589,934,592 deals in FreeCell Pro could be solved with five freecells. This turned out to be wrong too: Tom Holroyd ran the FCPro deals known to be impossible (with four freecells) through his solver, and number 14720822 turned out to be impossible with five freecells! This was the first known random deal to be impossible with five freecells (it is solvable with six).   Theodore Pringle and Shlomi Fish later found five more deals which require six freecells.

Note that 14720822 has only 7 cards covering the aces. Why is it so hard? Look at how many odd-numbered cards are at the bottoms of the columns, and how many of the even-numbered cards are clumped at the top.

David A. Miller has worked on making even harder deals than Adrian Ettlinger's, and has constructed some deals which appear to be impossible even with seven freecells. Here is one of his deals; Tom Holroyd's solver Patsolve says it is impossible, FreeCell Pro does not reach a conclusion:

Magic8
AS AD AC AH QS QD TS TD
5S 5D 3S 3D QC QH TC TH
5C 5H 3C 3H 8S 8D 6S 6D
9S 9D 7S 7D 8C 8H 6C 6H
9C 9H 7C 7H 4S 4D 2S 2D
KS KD JS JD 4C 4H 2C 2H
KC KH JC JH

Ryan L. Miller points out that a position can be reached, without filling any freecells, that requires ten freecells to solve. From the starting position below, move all 26 red cards to the homecells. The resulting position, with 26 black cards, needs ten freecells to win.

AC AS KS QS JS TS 9S 8S
2S 2C KC QC JC TC 9C 8C
3C 3S KH KD QH QD JH JD
4C 4S TH TD 9H 9D 8H 8D
5C 5S 7H 7D 6H 6D 5H 5D
6C 6S 4H 4D 3H 3D 2H 2D
7C 7S AH AD

He also says that it appears that at least 37 freecells are needed so that no unsolvable position can ever be reached. With 36 freecells, a blocked position can be reached in which the bottom row consists of all of the aces and queens, and the second row all kings and twos (each king covering an ace and each two a queen), and the other 36 cards are in freecells. Here's his example; this is actually a zero-freecell deal which can be trivially solved in 23 moves if played correctly.

AS AC AH AD QD QH QC QS
2D 2H 2S 2C KH KD KS KC
3S 3C 3H 3D JS JC JH JD
4H 4D 4S 4C TH TD TS TC
5S 5C 5H 5D 9S 9C 9H 9D
6H 6D 6S 6C 8H 8D 8S 8C
7S 7C 7H 7D

* What is a supermove? How does it help in playing?

Every good computer version of FreeCell allows the player to move a sequence of cards all at once using vacant freecells as momentary storage locations. This can also be done in related games of the Eight Off family. But in FreeCell (and Baker's Game), where any card may be placed in an empty column, even longer sequences can be moved using a combination of empty columns and empty freecells. Normally a sequence one card longer than the number of empty freecells can be moved from one column to another, but this is doubled for every empty column (except for the destination column -- if you are moving *to* an empty column, that column does not count). For example, a four-card sequence can be moved with three empty freecells, but if there is also a vacant column, an eight-card sequence can be moved, putting the first four cards temporarily in the empty column (using the freecells), then moving the other four cards to the destination (using the freecells again), and finally moving the first four cards from the formerly-empty column to the destination (using the freecells a third time).  Long sequence moves using empty columns as well as freecells have been called supermoves.

The most common and useful supermove situation is moving a four-card sequence from one column to another when there is an empty column but only one empty freecell. For example, if you want to move four cards from column 1 to column 2, with column 3 and freecell a empty, the sequence of moves one card at a time would be: 1a 13 a3 1a 12 a2 3a 32 a2. A move of this kind occurs at move 20 of the catalog solution to FC 617, and Richard Schiveley suggests that this is why so many people think the solution doesn't work -- if you are unfamiliar with supermoves, the move may look impossible, although Microsoft FreeCell carries it out with no difficulty.

FreeCell programs vary in their ability to use supermoves. The versions of Microsoft FreeCell, up through Windows XP, used supermoves correctly when there is one empty column and at least one empty freecell, but failed to make the maximum use of more than one empty column. When there are no empty freecells, but multiple empty columns, it treats the empty columns as freecells (e.g. three empty columns can be used to move an eight-card sequence even without any freecells, but MS FC only allows four to be moved). FreeCell Pro works correctly in all supermove situations, but when recording moves, converts complex supermoves into a series of individual moves compatible with the original versions of MS FC (the most common is a four-card sequence moved from a column to an empty column, when there is another empty column and one empty freecell.

* How many possible FreeCell deals are there?

Strictly speaking there are 52! different deals, about 8x10^67. However, deals can be transformed in several ways which make no mathematical difference, which cuts down the number a bit. The four left-hand (7 card) columns can be interchanged in 4! (24) ways, as can the four right-hand (6 card) columns. Also, suits can be interchanged in certain ways. If you swap suits so that all the black cards become red and vice versa (there are 4 ways to do this: SHCD can become HCDS, HSDC, DCHS, or DSHC respectively), the mathematical properties of the deal do not change; you can also maintain colors, but swap spades for clubs, diamonds for hearts, or both (3 more ways). So there are 576 permutations of columns (including no swaps) and 8 permutations of suits (including no swaps), which reduces the number of essentially different FreeCell deals to roughly 1.75x10^64 (a few rare deals will be identical under one of the 4608 transformations). The 32-bit integers used in FreeCell Pro and other programs can in theory generate 4294967296 deals, but the algorithm used by Microsoft and compatible programs repeats halfway through (FCPro uses a programming trick to get around this, and another trick to double this to 8589934592; it appears that these are all different). The solitaire package Hardwood Solitaire III, which includes FreeCell among its 100 games, actually allows in theory for any possible deal to be generated, but at the cost of having to enter a deal number of up to 68 digits. I do not know if Hardwood's New Deal function can actually select every single possible deal.

* What is the fewest number of cards one can have left remaining and still lose?

Since there are 12 places to put cards (eight columns and four freecells), *any* position with 12 cards or fewer is winnable. With plausible but careless play, it's possible (though fantastically unlikely) to have 13 cards left and lose. Here is an example worked out by David A. Miller, which finishes with only spades left (another example can be seen in deal number 2582 in the next question, if you play 32 instead of 42 on move 99!):

#15196 David A. Miller
5h 5h 8h 67 23 2a 27 27 27 2b
12 82 52 47 8c 83 48 c8 b8 63
6b 6c 67 a6 16 1a 12 b2 a2 5a
5h 7h 78 7b 75 65 76 1d 16 c6
b6 4h 7b 7h 3h 3h dh 4h 3c 3d
3h 8h 2h 37 31 1h ch 8c 8h 4h
6h 5h 21 2h 8h 2h 2h 62 6h 5h
85 8h 38

Madeleine Portwood writes that it seems to be possible to block all 13 cards of one suit in about 1 in 10 deals. There must be an ace in the bottom (deepest) row with a card of the same suit directly above it, and either another card of the same suit (or a king of another suit) directly above that, or two cards of the suit to be blocked at the bottom of another column -- this allows all of the other cards to be cleared.

Here's a different pattern, with 14 cards left, all hearts or diamonds:

#187 David A. Miller
3a 54 5b 35 35 3c 3d 61 71 71
7h c3 73 a7 27 8a d8 58 6h 5c
56 5d a5 65 25 d6 2a 24 2d 15
16 c2 82 81 a8 21 2a 43 d2 4c
4d 42 47 6h dh 5d 5h 3h c3 6h
67 64 62 86 82 a8 48 5h 3a 3h
14 12 4h 8h 2h 7a 7h 7c 4d 4h
7h 6h 83 87 7h bh 2b 2h 48 47
7h 27 2h 12

From a practical standpoint, I don't know of any magic number of cards left which makes victory even nearly certain. I've seen separate claims for 40 cards left and 36 cards left being sure wins, but I doubt either of these is true even as a general rule of thumb.

* Is it possible to play an entire suit to the homecells ahead of all of the other suits?

Yes. In fact, here is a solution in which all of the diamonds are played first, then all of the clubs:

#36 Michael Keller
81 8d 8c 8b 8a 52 a5 8a b8 d8
18 6b 1h 64 6d 67 c7 6c d6 c6
56 56 b6 a4 26 2a 2b 2h ah bh
57 1a 1h 71 7b 7c 7d 75 7h a7
d7 2a 27 26 c5 85 b2 68 6h a2
48 1a 1h 67 6h 1b 1h 6c 6h 16
26 12 54 5h 31 83 8h 45 4d 4h
d4 81 8h 18 38 31 3h 13 36 84
8h ah 7h bh ch 2h 56 41 45

Jason A. Crupper bettered this with a solution in which all four suits are played in order (32 instead of 42 on the next-to-last move blocks all 13 remaining spades):

#2582 Jason A. Crupper
8a 8b 83 8c 8d 83 b3 7b 78 a7
c7 d7 5a 25 25 1c 18 1d ch b1
4b 4h 4c 45 d5 b4 85 72 78 c8
71 27 2b 82 6c 68 68 b8 67 26
2b 2h 7h ah 7a 7h ch bh 1h 8b
8h 2h 12 1c b1 18 a1 61 32 3a
3b 32 56 3d 41 4h 5h bh ch dh
2h 7h 23 2h 78 7h 2b 2h 84 8h
53 6h 1c 1h 3h 1d 1h 38 3h 57
5h 35 3h 4h bh 4b 4h 2h 42 3c